题目内容
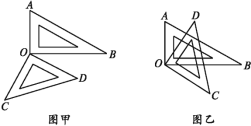
【题目】(1)将一副三角板按图甲的位置放置,那么∠AOD和∠BOC相等吗?∠AOC和∠BOD在数量上有何关系?说明理由.
(2)若将这副三角板按图乙所示摆放,三角板的直角顶点重合在点O处.上述关系还成立吗?
【答案】(1)∠AOD和∠BOC相等,∠AOC和∠BOD互补.理由见解析;(2)成立.理由见解析.
【解析】
(1)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时加上∠BOD可得∠AOD=∠COB;根据周角为360°且∠AOB=∠COD=90°,则∠AOC+∠BOD=360°90°90°=180°可得∠AOC和∠BOD互补;
(2)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时减去∠BOD可得∠AOD=∠COB;根据角的和差关系可得∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+90°=180°,进而可得∠BOD+∠AOC=180°
(1)∠AOD和∠BOC相等,∠AOC和∠BOD互补.
理由:
∵∠AOB=∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=360°-90°-90°=180°,
∴∠AOC和∠BOD互补.
(2)成立.
理由:
∵∠AOB=∠COD=90°,
∴∠AOB-∠BOD=∠COD-∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+∠BOD+∠COB=90°+∠DOC=90°+90°=180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目