题目内容
6．在一个不透明的口袋里，装有9个颜色不同其余都相同的球，其中有6个红球，2个蓝球和1个白球，将它们在口袋里搅匀；（1）从口袋一次任意取出4个球，一定有红球，这是一个必然事件
（2）从口袋任意取出1个球，恰好红球的概率是多少？
（3）从上述9个球中任取几个来设计一个游戏，使得摸到红球的概率为$\frac{1}{3}$．写出你的设计方案．
分析 事件的可能性主要看事件的类型，事件的类型决定了可能性及可能性的大小．
解答 解：（1）∵口袋里有2个蓝球和1个白球，其它的是红球，
∴从口袋一次任意取出4个球，一定有红球，这是一个必然事件；
（2）∵口袋里装有9个颜色不同其余都相同的球，其中有6个红球，
∴恰好红球的概率是$\frac{6}{9}$=$\frac{2}{3}$；
（3）从上述9个球中任取几个，设计一个游戏，使得摸到红球的概率为$\frac{1}{3}$，那么它们的个数为2个红球，2个蓝球和2个白球．
点评 本题主要考查概率公式和随机事件，必然事件指在一定条件下一定发生的事件；不可能事件是指在一定条件下，一定不发生的事件；不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．用到的知识点为：可能性等于所求情况数与总情况数之比．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
16．如图是某单位考核情况条形统计图（A、B、C三个等级），则下面的回答正确的是（ ）
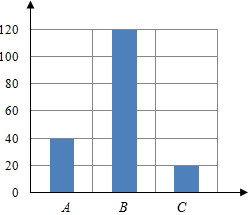
| A． | C等人最少，占总数的30% | B． | 该单位共有120人 | ||
| C． | A等人比C等多10% | D． | B等人最多，占总人数的$\frac{2}{3}$ |
14．力帆集团原计划生产某一型号的汽车8000辆，为了提高效率，企业改进了技术，现每天可比原计划多生产40辆汽车，结果提前10天完成了生产计划．若设原计划需要x天完成，则根据题意列方程为（ ）
| A． | $\frac{8000}{x}$-$\frac{8000}{x+10}$=40 | B． | $\frac{8000}{x+10}$-$\frac{8000}{x}$=40 | ||
| C． | $\frac{8000}{x-10}$=$\frac{8000}{x}$+40 | D． | $\frac{8000}{x-10}$=$\frac{8000}{x}$-40 |
1．
如图，在矩形ABCD中，点E在AD上，且EC平分∠BED，AB=2，∠ABE=45°，则DE的长为（ ）
如图，在矩形ABCD中，点E在AD上，且EC平分∠BED，AB=2，∠ABE=45°，则DE的长为（ ）| A． | 2$\sqrt{2}$-2 | B． | $\sqrt{\frac{1}{2}}$-1 | C． | $\sqrt{3}$-1 | D． | 2-$\sqrt{2}$ |
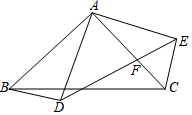如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形，DE交AC于点F．