Question

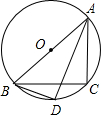已知：如图，AB是⊙O的直径，C是⊙O上的一点，∠BAC的平分线交⊙O于D，若∠ABC=40°，则∠ABD=________度．

Answer 1

65
分析：首先根据AB是直径，由圆周角定理得出∠ACB是直角，进而可求出∠BAC、∠DAC的度数；然后根据同弧所对的圆周角相等，求得∠DBC的度数，从而由∠ABD=∠ABC+∠DBC得到∠ABD的度数．
解答：∵AB是⊙O的直径，
∴∠ACB=90°，即∠BAC+∠ABC=90°；
∴∠BAC=50°；
∵AD平分∠BAC，
∴∠DAC=∠BAC=25°；
∴∠DBC=∠DAC=25°；
故∠ABD=∠ABC+∠DBC=65°．
点评：此题主要考查的是圆周角定理的推论；
半圆（弧）和直径所对的圆周角是直角；同弧所对的圆周角相等．