题目内容
如图,直线 与
与 轴、
轴、 轴分别相交于点
轴分别相交于点 、
、 .抛物线
.抛物线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于 、
、 ,且
,且 .
.

(1)求点 、
、 、
、 的坐标;
的坐标;
(2)如果 ,求抛物线
,求抛物线 的解析式.
的解析式.
 与
与 轴、
轴、 轴分别相交于点
轴分别相交于点 、
、 .抛物线
.抛物线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于 、
、 ,且
,且 .
.
(1)求点
 、
、 、
、 的坐标;
的坐标;(2)如果
 ,求抛物线
,求抛物线 的解析式.
的解析式.(1) (
( ,0),
,0), (0,1),
(0,1), (0,3)(2)
(0,3)(2)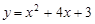
 (
( ,0),
,0), (0,1),
(0,1), (0,3)(2)
(0,3)(2)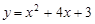
(1) (
( ,0),
,0), (0,1),
(0,1),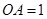 , 在Rt△
, 在Rt△ 中,∵
中,∵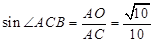 ,
,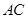 =
=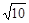 ,
,
∴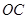 =
=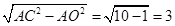
∴点 的坐标(0,3).
的坐标(0,3).
(2)当点 在
在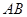 延长线上时,
延长线上时,
∵ (0,1),
(0,1),
∴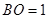 ,
,
∴ ,
,
∵ ,
,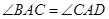 ,
,
∴△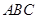 ∽△
∽△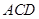 .
.
∴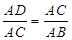 ,
,
∴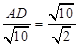 ,
,
∴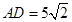 .
.
过点 作
作 ⊥
⊥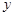 轴,垂足为
轴,垂足为 ,
,
∵ //
// ,
,
∴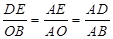 ,
,
∴ .
.
∴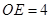 ,
,
∴点 的坐标为(4,5).
的坐标为(4,5).
设二次函数的解析式为 ,∴
,∴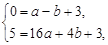
∴
∴二次函数解析式为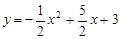 .
.
当点 在射线
在射线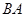 上时,同理可求得点
上时,同理可求得点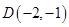 ,
,
二次函数解析式为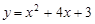 .
.
评分说明:过点 作
作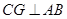 于
于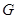 ,当点
,当点 在
在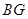 延长线上或点
延长线上或点 在射线
在射线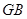 上时,可用锐角三角比等方法得
上时,可用锐角三角比等方法得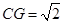 (1分),
(1分),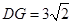 (1分),另外分类有1分其余同上.
(1分),另外分类有1分其余同上.
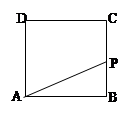
(1)设一次函数中的y=0,求出x的值,即A的横坐标,设x=0,求出y的值即B的纵坐标,再利用已知条件和勾股定理求出OC的长,即C的纵坐标;
(2)因为如果∠CDB=∠ACB,则D点的位置不确定,因此小题需要分①当点D在AB延长线上时,②当点D在射线BA上时,两种情况讨论,求出满足题意的抛物线y=ax2+bx+c的解析式即可.
 (
( ,0),
,0), (0,1),
(0,1),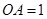 , 在Rt△
, 在Rt△ 中,∵
中,∵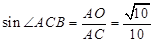 ,
,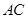 =
=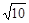 ,
,∴
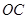 =
=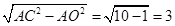
∴点
 的坐标(0,3).
的坐标(0,3).(2)当点
 在
在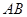 延长线上时,
延长线上时,∵
 (0,1),
(0,1),∴
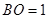 ,
,∴
 ,
,∵
 ,
,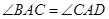 ,
,∴△
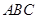 ∽△
∽△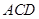 .
. ∴
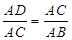 ,
,∴
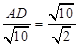 ,
,∴
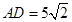 .
. 过点
 作
作 ⊥
⊥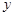 轴,垂足为
轴,垂足为 ,
,∵
 //
// ,
,∴
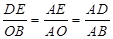 ,
,∴
 .
.∴
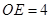 ,
,∴点
 的坐标为(4,5).
的坐标为(4,5). 设二次函数的解析式为
 ,∴
,∴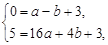
∴

∴二次函数解析式为
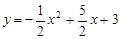 .
. 当点
 在射线
在射线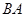 上时,同理可求得点
上时,同理可求得点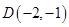 ,
, 二次函数解析式为
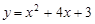 .
. 评分说明:过点
 作
作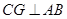 于
于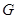 ,当点
,当点 在
在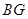 延长线上或点
延长线上或点 在射线
在射线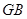 上时,可用锐角三角比等方法得
上时,可用锐角三角比等方法得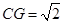 (1分),
(1分),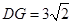 (1分),另外分类有1分其余同上.
(1分),另外分类有1分其余同上.(1)设一次函数中的y=0,求出x的值,即A的横坐标,设x=0,求出y的值即B的纵坐标,再利用已知条件和勾股定理求出OC的长,即C的纵坐标;
(2)因为如果∠CDB=∠ACB,则D点的位置不确定,因此小题需要分①当点D在AB延长线上时,②当点D在射线BA上时,两种情况讨论,求出满足题意的抛物线y=ax2+bx+c的解析式即可.

练习册系列答案
相关题目
 的解,点C是直线
的解,点C是直线 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=
 的图像经过点
的图像经过点 (1,-5),且与直线
(1,-5),且与直线 平行,那么该一次函数的解析式为 .
平行,那么该一次函数的解析式为 . 的图象为
的图象为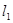 ,一次函数
,一次函数 的图象为直线
的图象为直线 ,若
,若 ,且
,且 ,我们就称直线
,我们就称直线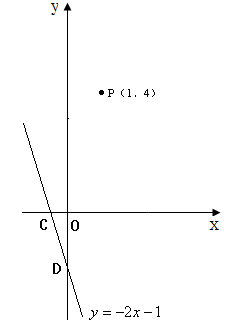
 平行的直线的函数表达式,并画出直
平行的直线的函数表达式,并画出直 轴、y轴交于A、B两点,直线
轴、y轴交于A、B两点,直线



 、
、 、……、
、……、 都在直线
都在直线 上,若这n个点的横坐标的平均数为a,则这n个点的纵坐标的平均数为 。
上,若这n个点的横坐标的平均数为a,则这n个点的纵坐标的平均数为 。 中,
中, 的值随
的值随 的增大而减小,则
的增大而减小,则 的取值范围是( )
的取值范围是( )



