Question

【题目】如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于（ ）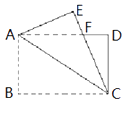

A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：由题意得：
EC=BC=6，AE=AB=4，∠BCA=∠FCA，
∵四边形ABCD是矩形，
∴AD∥BC,AB=CD,
∴∠FAC=∠BCA,
∴∠FAC=∠FCA,
∴AF=CF，
∴AD-AF=CE-CF，
即DF=FE．
设DF=FE=x，CF=6-x，
在Rt△CDF中， ．
即 ，
解得：x=,
即DF=.
故选B.
【考点精析】利用等腰三角形的性质和矩形的性质对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；矩形的四个角都是直角，矩形的对角线相等．