题目内容
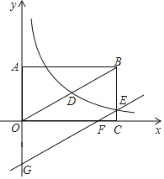
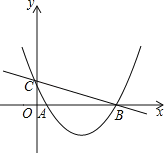
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 和点
和点![]() .
.
(1)求抛物线的解析式;
(2)求直线![]() 的解析式;
的解析式;
(3)若点![]() 是抛物线上的动点,过点
是抛物线上的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,以
,以![]() ,
,![]() ,
,![]() 为顶点的三角形是否能够与
为顶点的三角形是否能够与![]() 相似(排除全等的情况)?若能,请求出所有符合条件的点
相似(排除全等的情况)?若能,请求出所有符合条件的点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)抛物线的解析式为![]() ;
;
(2)直线![]() 的解析式
的解析式![]() ;
;
(3)![]() 点的坐标为
点的坐标为![]() 、
、![]() 或
或![]() .
.
【解析】
(1)把点![]() 坐标代入抛物线
坐标代入抛物线![]() 求得抛物线的解析式即可;
求得抛物线的解析式即可;
(2)求出抛物线的对称轴,再求得点![]() 、
、![]() 坐标,设直线
坐标,设直线![]() 的解析式为
的解析式为![]() ,再把
,再把![]() 两点坐标代入线
两点坐标代入线![]() 的解析式为
的解析式为![]() ,求得
,求得![]() 和
和![]() 即可;
即可;
(3)设![]() ,分两种情况讨论:①
,分两种情况讨论:①![]() ,②
,②![]() ,根据相似,得出比例式,再分别求得点
,根据相似,得出比例式,再分别求得点![]() 坐标即可.
坐标即可.
解:(1)![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)抛物线的对称轴为直线![]() ,
,
![]() 点
点![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() 把
把![]() 、
、![]() 两点坐标代入线
两点坐标代入线![]() 的解析式为
的解析式为![]() ,得
,得
![]() ,
,
解得![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式
的解析式![]() ;
;
(3)设![]() ,分三种情况讨论:
,分三种情况讨论:
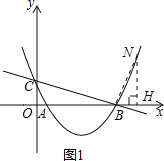
①当![]() 时,如图1,
时,如图1,
![]() ,
,
即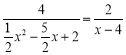 ,
,
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
![]() 点
点![]() 坐标
坐标![]() ;
;
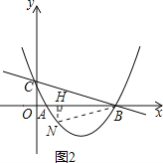
②当![]() 时,如图2,
时,如图2,
![]() ,
,
即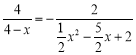 ,
,
解得![]() ,
,![]() (不合题意舍去),
(不合题意舍去),
![]() 点
点![]() 坐标
坐标![]() ;
;
③当![]() 在第二象限时,如下图
在第二象限时,如下图
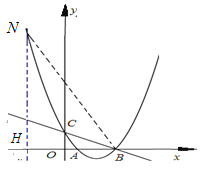
![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
即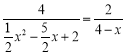 ,
,
得到![]()
解得![]() (舍去);
(舍去);![]() ,
,
![]() 点的坐标为
点的坐标为![]()
综上所述,![]() 点的坐标为
点的坐标为![]() 、
、![]() 或
或![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目