题目内容
如图，在6×8的网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1：2
⑵连接⑴中的AA′，求四边形AA′C′C的周长.（结果保留根号）
【答案】
（1）3+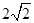
+
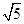；（2）3.
【解析】
试题分析：（1）以O为位似中心，作△ABC的位似图形，使相似比为1：2，
（2）根据所作三角形三点的位置写出对应三角形边长，进而求出三角形周长和面积．
试题解析：（1）如图所示：
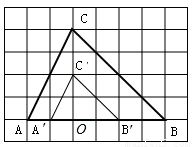
（2）如图所示：
∵B′C′=3，A′O=2，A′B′=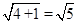
，A′C′=
，
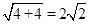∴△A′B′C′的周长为：3++，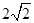
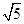△A′B′C′的面积为：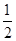
×A′O×B′C′=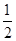×2×3=3．
考点:作图――位似变换．
练习册系列答案
口算能手系列答案
相关题目
13、如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出△OAB的一个位似图形，使两个图形以O为位似中心，且所画图形与△OAB的位似比为2：1．
7、如图，在8×12的网格图中（每个小正方形的边长均为1cm），点A、B在格点上，⊙A、⊙B的半径都为1cm．若⊙A以每秒1cm的速度自左向右运动，与此同时，⊙B的半径在不断增大，它的半径r（cm）与时间t（s）之间的关系式为r=1+t（t≥0），则在网格图范围内，当两圆相切时，t的值为（ ）
23、如图，在10×6的网格图中（每个小正方形的边长均为1个单位长）．⊙A半径为2，⊙B半径为1，需使⊙A与静止的⊙B相切，那么⊙A由图示的位置需向左平移多少个单位长．
（2009•九龙坡区一模）如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上．
如图，在6×10的网格中，△DEF是△ABC平移后的图形那么△ABC经过（ ）而得到△DEF：