题目内容
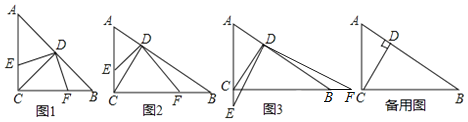
【题目】如图，在
中，
，
，
于点D，点E是直线AC上一动点，连接DE，过点D作
，交直线BC于点F．
探究发现：
如图1，若
，点E在线段AC上，则
______；
数学思考：
如图2，若点E在线段AC上，则______
用含m，n的代数式表示
；
当点E在直线AC上运动时，中的结论是否任然成立？请仅就图3的情形给出证明；
拓展应用：若
，
，
，请直接写出CE的长．
【答案】（1）1；
；（2）①；②；（3）
或
．
【解析】分析：(1)先用等量代换判断出
，
，得到
∽
，再判断出
∽
即可；(2)方法和
一样，先用等量代换判断出，，得到∽，再判断出∽即可；(3)由
的结论得出∽，判断出
，求出DE，再利用勾股定理，计算出即可．
详解：当
时，即：
，
，
，
，
，
，
，
，
即，
∽，
，
，
，
∽，
，
，
，
，
，
，
，
，
即，
∽，
，
，，
∽，
，
成立
如图，
，
，
又，
，
，
，
，
即，
∽，
，
，，
∽，
，
．
由有，∽，
，
，
，
在
中，
，
，
，
当E在线段AC上时，在
中，
，
，
根据勾股定理得，
，
，或
舍
当E在直线AC上时，
在中，
，，
根据勾股定理得，，
，
，或
舍，
即：或．
练习册系列答案
相关题目
