Question

【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足,,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发．

（1）求a、b的值

（2）当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度

（3）在的条件下,当P、Q两点间的距离是6个单位长度时,求OP的长．

Answer 1

【答案】（1），；（2）点Q的运动速度每秒1个单位长度；（3）OP的长为或．

【解析】

由点C表示7,可得,由,,得A、B两点表示的数,可得a、b的值；

先计算P运动时间,根据点Q运动的位置恰好是线段AB靠近点B的三等分点,可知：,可得点Q的路程,根据时间可得结论；

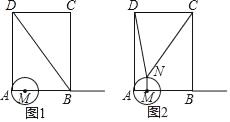
设t秒时,,分两种情况：如图1,当Q在P的右侧时,如图2,当Q在P的左侧时；根据分别列式可得t的值,再计算OP的长．

解：,

点A表示的数为,即,

表示的数为7,

,

,

,

点B表示的数为6,即；.

当P为OB的中点时,

,

,

由题意得：,

,

,

答：点Q的运动速度每秒1个单位长度；.

设t秒时,,

分两种情况：

如图1,当Q在P的右侧时,

,

,

,

,

,

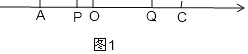
如图2,当Q在P的左侧时,

,

,

,

,

,

综上所述,OP的长为或．