题目内容
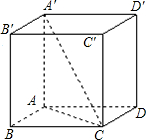如图，在长方体ABCD-A′B′C′D′中，△A′AC是直角三角形，若AA′=1，AB=BC=2，则A′C=________．
3
分析：先在Rt△ABC中利用勾股定理求出AC，再在Rt△A′AC中利用勾股定理可求A′C．
解答：在Rt△ABC中，AC=
=
=2
，
在Rt△A′AC中，A′C=
=
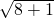=3．
故答案是3．
点评：本题考查了勾股定理．解题的关键是知道△ABC、△A′AC是直角三角形．
分析：先在Rt△ABC中利用勾股定理求出AC，再在Rt△A′AC中利用勾股定理可求A′C．
解答：在Rt△ABC中，AC=
==2，在Rt△A′AC中，A′C=
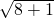==3．故答案是3．
点评：本题考查了勾股定理．解题的关键是知道△ABC、△A′AC是直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、如图，在长方体ABCD-EFGH中，与平面ADHE垂直的棱共有
5、如图，在长方体ABCD-EFGH中，与面ABFE垂直的棱有（ ）
14、如图，在长方体ABCD-EFGH中，与平面ADHE和平面CDHG都平行的棱为
如图，在长方体ABCD-EFGH中，棱AD与面DCGH的位置关系是