题目内容
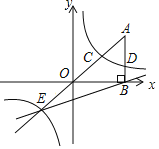
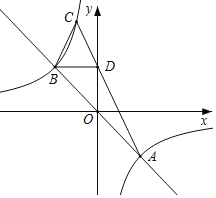
【题目】如图，直线y=﹣x与反比例函数y=
的图象交于A，B两点，过点B作BD∥x轴，交y轴于点D，直线AD交反比例函数y=的图象于另一点C，则
的值为（ ）
A. 1：3 B. 1：2
C. 2：7 D. 3：10
【答案】A
【解析】联立直线AB与反比例函数解析式成方程组，通过解方程组可求出点A、B的坐标，由BD∥x轴可得出点D的坐标，由点A、D的坐标利用待定系数法可求出直线AD的解析式，联立直线AD与反比例函数解析式成方程组，通过解方程组可求出点C的坐标，再结合两点间的距离公式即可求出
的值．
联立直线AB及反比例函数解析式成方程组，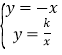
，
解得：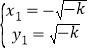
，
，
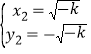∴点B的坐标为（﹣
，），点A的坐标为（，﹣），
∵BD∥x轴，
∴点D的坐标为（0，）．
设直线AD的解析式为y=mx+n，
将A（，﹣）、D（0，）代入y=mx+n，
，解得：
，
∴直线AD的解析式为y=﹣2+，
联立直线AD及反比例函数解析式成方程组，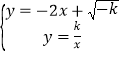
，
解得：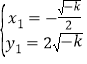
，，
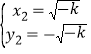∴点C的坐标为（﹣
，2）．
∴
，
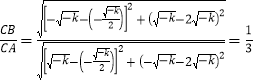故选A．
练习册系列答案
应用题作业本系列答案
相关题目
