Question

【题目】已知经过原点的抛物线与轴的另一个交点为，现将抛物线向右平移个单位长度，所得抛物线与轴交于，与原抛物线交于点，设的面积为，则用表示=__________

Answer 1

【答案】

【解析】试题解析：令-2x2+4x=0，得x1=0，x2=2

∴点A的坐标为（2，0），

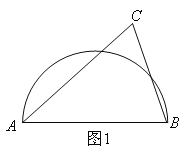
如图1，当0＜m＜2时，作PH⊥x轴于H，

设P（xP，yP），

∵A（2，0），C（m，0）

∴AC=2-m，

∴CH=

∴xP=OH=m+

把xP=代入y=-2x2+4x，

得yP=-m2+2

∵CD=OA=2

∴S=CDHP=×2×（-m2+2）=-m2+2

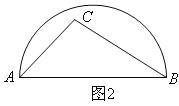
如图2，当m＞2时，作PH⊥x轴于H，

设P（xP，yP）

∵A（2，0），C（m，0）

∴AC=m-2，

∴AH=

∴xP=OH=2+=

把xP=代入y=-2x2+4x，得

yP=-m2+2

∵CD=OA=2

∴S=CDHP=m2-2．

综上可得：s＝．