题目内容
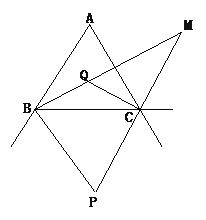
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
【答案】![]()
【解析】
已知CQ、CM分别是∠ACB及其外角的平分线,可得∠QCM=90°,由题意可得∠BQC=90°+![]() ∠A,根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,由此即可求得∠ A和∠M的关系.
∠A,根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,由此即可求得∠ A和∠M的关系.
∵CQ、CM分别是∠ACB及其外角的平分线,
∴∠QCM=90°,
由题意可得∠BQC=90°+![]() ∠A,
∠A,
根据三角形外角的性质可得,∠BQC=∠QCM+∠M=90°+∠M,
∴90°+![]() ∠A=90°+∠M,
∠A=90°+∠M,
∴![]() ∠A=∠M.
∠A=∠M.
故答案为:![]() .
.

练习册系列答案
相关题目