Question

如图，抛物线的顶点坐标为，并且与y轴交于点C，与x轴交于两点A,B.

  （1）求抛物线的表达式；

  （2）设抛物线的对称轴与直线BC交于点D，连结AC、AD, 求△ACD的面积；

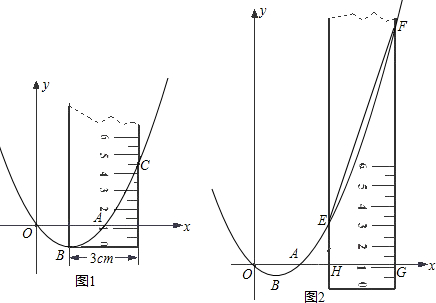
  （3）点E位直线BC上一动点，过点E作y轴的平行线EF，与抛物线交于点F.问是否存

  在点E，使得以D、E、F为顶点的三角形与△BCO相似.若存在，求出点E的坐标；若不存

  在，请说明理由.

    

Answer 1

（1）由题意可设抛物线的表达式为.

∵点C在抛物线上，

∴，解得.

∴抛物线的表达式为，即

（2）令，即，解得，

∴.

设BC的解析式为将代入得，解得.

∴直线BC的解析式为

当时，，∴.

所以－－

(1)  假设存在点E，使得以D、E、F为顶点的三角形与△BCO相似，

∵△BCO是等腰直角三角形，

则以D、E、F为顶点的三角形也必须是等腰直角三角形.

由EF∥OC得∠DEF=45°，故以D、E、F为顶点的等腰直角三角形

只能以点D、F为直角顶点