题目内容
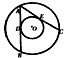
 如图,O为两同心圆圆心,点A为大圆上一点,点B为小圆上一点,且∠ABO=90°,AB=3,则该圆环的面积为
如图,O为两同心圆圆心,点A为大圆上一点,点B为小圆上一点,且∠ABO=90°,AB=3,则该圆环的面积为
- A.
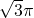
- B.3π
- C.9π
- D.6π
C
分析:令大圆的半径为R,小圆的半径为r,圆环的面积=大圆的面积-小圆的面积=π(R2-r2);由∠ABO=90°,AB=3,利用勾股定理,R2-r2=AB2,问题解决.
解答:设大圆的半径为R,小圆的半径为r,则
圆环的面积=π(R2-r2)①;
∵∠ABO=90°,AB=3,
∴△ABO是直角三角形,
∴R2-r2=AB2=32=9②.
∴由①②得圆环的面积=9π.
故选C.
点评:该题运用了圆环的面积求法,巧妙地和勾股定理结合将问题解决.
分析:令大圆的半径为R,小圆的半径为r,圆环的面积=大圆的面积-小圆的面积=π(R2-r2);由∠ABO=90°,AB=3,利用勾股定理,R2-r2=AB2,问题解决.
解答:设大圆的半径为R,小圆的半径为r,则
圆环的面积=π(R2-r2)①;
∵∠ABO=90°,AB=3,
∴△ABO是直角三角形,
∴R2-r2=AB2=32=9②.
∴由①②得圆环的面积=9π.
故选C.
点评:该题运用了圆环的面积求法,巧妙地和勾股定理结合将问题解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,O为两同心圆圆心,点A为大圆上一点,点B为小圆上一点,且∠ABO=90°,AB=3,则该圆环的面积为( )
如图,O为两同心圆圆心,点A为大圆上一点,点B为小圆上一点,且∠ABO=90°,AB=3,则该圆环的面积为( )A、
| ||
| B、3π | ||
| C、9π | ||
| D、6π |



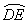 的度数为110°,则
的度数为110°,则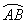 的度数为
的度数为