题目内容
如图,点M(2,a)在反比例函数y=
 的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )
的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )


A.3 B.
 C.6 D.2
C.6 D.2

D【考点】反比例函数图象上点的坐标特征.
【分析】先求出M的坐标,根据对称性求出N的坐标,再根据勾股定理求出即可.
【解答】解:

过M作x轴的垂线,过N作y轴的垂线,两线交于E,
把(2,a)代入反比例函数y=
 得:a=3,
得:a=3,
即M的坐标为(2,3),
所以N的坐标为(﹣2,﹣3),
则ME=3﹣(﹣3)=6,NE=2﹣(﹣2)=4,
所以MN=
 =2
=2
 ,
,
故选D.
【点评】本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,能求出M、N的坐标是解此题的关键,数形结合思想的应用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ,则x 的值等于____________.
,则x 的值等于____________.

 中,
中, ,以
,以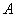 为圆心,
为圆心, 为半径画弧交线段
为半径画弧交线段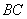 于
于 ,连接
,连接 ,则阴影部分的面积为( ).
,则阴影部分的面积为( ). B.
B. C.
C. D.
D.

