题目内容
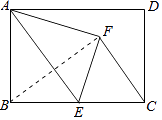
【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别
从A、C两点同时以1cm/s的相同的速度向C、A运动.

(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,
四边形DEBF为矩形.
【答案】(1)四边形DEBF是平行四边形(2) 当运动时间t为3或13s时.四边形DEBF为矩形
【解析】试题分析:(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:16-t-t=10或2t-16=10,继而求得答案.
解:(1)四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形.
∴OA=OC.OB=OD.
∵E.F是AC上两动点.E.F分别从A.C两点同时以1cm/s的相同的速度向C.A运动.
∴AE=CF.
∴OE=OF.
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=tcm.
∵四边形DEBF是平行四边形.
∴当EF=BD时.四边形DEBF为矩形.
即AC-AE-CF=BD.
∴16-t-t=10或2t-16=10
解得:t=3.或t=13
∴当运动时间t为3或13s时.四边形DEBF为矩形

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |

(1)表格中a的值为 , b的值为 .
(2)扇形统计图中表示获得一等奖的扇形的圆心角为度.
(3)估计全市有多少名学生获得三等奖?
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
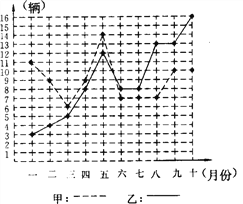
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).