题目内容
如图,函数![]() 的图象与函数
的图象与函数![]() (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.

(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
(1)60(2)52.8km/h(3)3.35 (L)
【解析】解:(1)60。
(2)当20£x£30时,设y与x之间的函数关系式为y=kx+b。
根据题意,当x=20时,y=60;当x=30时,y=24。
∴![]() ,解得
,解得![]() 。
。
∴当20£x£30时,y与x之间的函数关系式为y= -3.6x+132。
∵当x=22时,y= -3.6´22+132=52.8,
∴小丽出发第22min时的速度为52.8km/h。
(3)小丽驾车从甲地到乙地行驶的路程为

∵汽车每行驶100 km耗油10 L,
∴小丽驾车从甲地到乙地共耗油![]() (L) 。
(L) 。
(1)观察图象可知,第10min到20min之间的速度最高。
(2)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答,再把x=22代入函数关系式进行计算即可得解。
(3)用各时间段的平均速度乘以时间,求出行驶的总路程,再乘以每千米消耗的油量即可。

练习册系列答案
相关题目
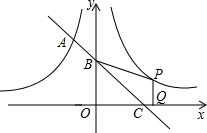 如图,一次函数的图象与反比例函数
如图,一次函数的图象与反比例函数 的图象经过A(2, 0)、B(0,-6)两点。
的图象经过A(2, 0)、B(0,-6)两点。 
 的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值. 的图象与
的图象与 的图象关于y轴对称,在y2=
的图象关于y轴对称,在y2= 的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
的图象上取一点P(P点的横坐标大于2),过P作PQ丄x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当 时,一次函数值大于反比例函数值,当
时,一次函数值大于反比例函数值,当 时,一次函数值小于反比例函数值.
时,一次函数值小于反比例函数值.
 (x>0)的图象与
(x>0)的图象与