题目内容
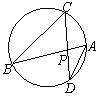
如图,AB是⊙O的直径,C是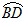 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.
(1)试判断∠A与∠BCE的关系,并进行说明;(5分)
(2)求证:BF = CF.(5分)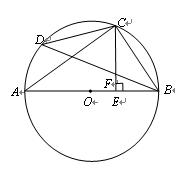
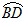 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.(1)试判断∠A与∠BCE的关系,并进行说明;(5分)
(2)求证:BF = CF.(5分)

(1)∠A = ∠BCE,理由如下:
∵ AB是⊙O的直径,
∴∠ACB = 90°,
∴∠A +∠ABC = 90°
又∵ CE⊥AB,
∴ ∠CEB = 90°,∴∠BCE +∠ABC = 90°
∴∠A = ∠BCE.
(2)∵ C是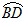 的中点,
的中点,
∴ 弧CD =弧CB
∴ ∠CBD = ∠A
∵∠A = ∠BCE
∴ ∠BCE = ∠CBD,
∴ BF = CF.
∵ AB是⊙O的直径,
∴∠ACB = 90°,
∴∠A +∠ABC = 90°
又∵ CE⊥AB,
∴ ∠CEB = 90°,∴∠BCE +∠ABC = 90°
∴∠A = ∠BCE.
(2)∵ C是
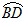 的中点,
的中点,∴ 弧CD =弧CB
∴ ∠CBD = ∠A
∵∠A = ∠BCE
∴ ∠BCE = ∠CBD,
∴ BF = CF.
(1)由AB是⊙O的直径,得到∠ACB=90°,而CE⊥AB,利用同角的余角相等可得∠A=∠BCE;
(2)由C是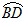 的中点,得∠CBD=∠A,由(1)的结论有∠BCE=∠CBD,于是得到BF=CF.
的中点,得∠CBD=∠A,由(1)的结论有∠BCE=∠CBD,于是得到BF=CF.
(2)由C是
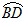 的中点,得∠CBD=∠A,由(1)的结论有∠BCE=∠CBD,于是得到BF=CF.
的中点,得∠CBD=∠A,由(1)的结论有∠BCE=∠CBD,于是得到BF=CF.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.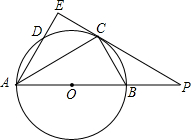
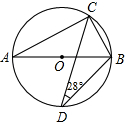
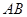 和
和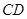 相交于点
相交于点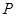 ,
,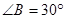 ,
,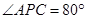 ,则
,则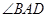 的度数为( )
的度数为( )