题目内容
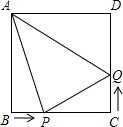
在边长为10m的正方形的池塘边上的A,B,C,D处各有一棵树,已知AB=1m,BC=2m,CD=3m.现用一根长4m的绳子将一头羊拴在某一棵树上,为了使羊的活动区域最大(羊不能下水),应将绳子拴在________处的树上.

B
分析:分别计算拴在A,B,C,D处的树上羊活动区域的面积.当绳子拴在A处的树上,则羊活动区域分两部分:以A为圆心,4为半径的半圆和以B为圆心,3为半径,圆心角为90°的扇形;当绳子拴在B处的树上,则羊活动区域为以B为圆心,4为半径,圆心角为270°的扇形;当绳子拴在C处的树上,则羊活动区域分两部分:以C为圆心,4为半径的半圆和以C为圆心,2为半径,圆心角为90°的扇形;当绳子拴在D处的树上,则羊活动区域为:以D为圆心,4为半径的半圆.然后分别利用扇形和圆的面积公式计算即可得到答案.
解答:当绳子拴在A处的树上,则羊活动区域分两部分:以A为圆心,4为半径的半圆和以B为圆心,3为半径,圆心角为90°的扇形,所以SA= π×42+
π×42+ =
= ;
;
当绳子拴在B处的树上,则羊活动区域为以B为圆心,4为半径,圆心角为270°的扇形,所以SB= =12π;
=12π;
当绳子拴在C处的树上,则羊活动区域分两部分:以C为圆心,4为半径的半圆和以C为圆心,2为半径,圆心角为90°的扇形,所以SC= π×42+
π×42+ =9π;
=9π;
当绳子拴在D处的树上,则羊活动区域为:以D为圆心,4为半径的半圆,所以SD= π×42=8π;
π×42=8π;
所以有SD<SC<SA<SB,即为了使羊的活动区域最大(羊不能下水),应将绳子拴在B处树上.
故答案为B.
点评:本题考查了扇形的面积公式:S= ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.
lR,l为扇形的弧长,R为半径.
分析:分别计算拴在A,B,C,D处的树上羊活动区域的面积.当绳子拴在A处的树上,则羊活动区域分两部分:以A为圆心,4为半径的半圆和以B为圆心,3为半径,圆心角为90°的扇形;当绳子拴在B处的树上,则羊活动区域为以B为圆心,4为半径,圆心角为270°的扇形;当绳子拴在C处的树上,则羊活动区域分两部分:以C为圆心,4为半径的半圆和以C为圆心,2为半径,圆心角为90°的扇形;当绳子拴在D处的树上,则羊活动区域为:以D为圆心,4为半径的半圆.然后分别利用扇形和圆的面积公式计算即可得到答案.
解答:当绳子拴在A处的树上,则羊活动区域分两部分:以A为圆心,4为半径的半圆和以B为圆心,3为半径,圆心角为90°的扇形,所以SA=
 π×42+
π×42+ =
= ;
;当绳子拴在B处的树上,则羊活动区域为以B为圆心,4为半径,圆心角为270°的扇形,所以SB=
 =12π;
=12π;当绳子拴在C处的树上,则羊活动区域分两部分:以C为圆心,4为半径的半圆和以C为圆心,2为半径,圆心角为90°的扇形,所以SC=
 π×42+
π×42+ =9π;
=9π;当绳子拴在D处的树上,则羊活动区域为:以D为圆心,4为半径的半圆,所以SD=
 π×42=8π;
π×42=8π;所以有SD<SC<SA<SB,即为了使羊的活动区域最大(羊不能下水),应将绳子拴在B处树上.
故答案为B.
点评:本题考查了扇形的面积公式:S=
 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.
lR,l为扇形的弧长,R为半径. 
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目