题目内容
5.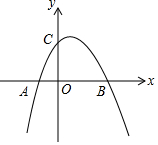 如图,二次函数y=-x2+2x+k的图象经过点C(0,6),与x轴交于A,B两点
如图,二次函数y=-x2+2x+k的图象经过点C(0,6),与x轴交于A,B两点(1)k=6;
(2)根据图象写出一元二次方程-x2+2x+k=0的根.
分析 (1)利用待定系数法即可解决问题.
(2)求出A、B两点坐标,即可解决问题.
解答 解:(1)∵二次函数y=-x2+2x+k的图象经过点C(0,6),
∴k=6,
故答案为6.
(2)对于抛物线y=-x2+2x+6,令y=0,得到二次函数-x2+2x+6=0,解得x=1±$\sqrt{7}$,
∴A(1-$\sqrt{7}$,0),B(1+$\sqrt{7}$,0),
一元二次方程-x2+2x+k=0的根,就是二次函数的图象与x轴交点的横坐标,
∴一元二次方程-x2+2x+k=0的根为1±$\sqrt{7}$.
点评 本题考查抛物线与x轴的交点、一元二次方程与二次函数的关系等知识,解题的关键是灵活运用所学知识,搞清楚二次函数与一元二次方程之间的关系,属于中考常考题型.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.若“神舟十一号”飞船发射点火前10秒记为-10秒,那么发射点火后15秒应记为( )
| A. | 15 | B. | -15 | C. | 5 | D. | -5 |
13.计算(-36)÷(-6)的结果为( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
20.下列运算正确的是( )
| A. | 4a2-2a2=2 | B. | 5a2•a4=5a8 | C. | a7÷a3=a4 | D. | (a2b3)2=a4b5 |
16. 如图,点A,B在数轴上对应的实数分别为m,n,则m-n( )0.
如图,点A,B在数轴上对应的实数分别为m,n,则m-n( )0.
 如图,点A,B在数轴上对应的实数分别为m,n,则m-n( )0.
如图,点A,B在数轴上对应的实数分别为m,n,则m-n( )0.| A. | 大于 | B. | 小于 | C. | 等于 | D. | 不能确定 |
13.若代数式x2-3x的值为12,则代数式$\frac{1}{3}$x2-x+2014的值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
13.下列运算中结果正确的是( )
| A. | 3a+2b=5ab | B. | 5y-3y=2 | C. | 2x2y-3x2y=-x2y | D. | -3x+5x=-8x |
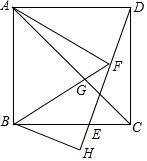 在正方形ABCD中,点E为BC边上的一点,连接DE,点F为DE的中点,连接FA、FB,线段FB与AC交于点G,过B作BH⊥DE交DE的延长线于点H,若BH=3,AG:GC=$\sqrt{3}$:1,则△AFG的面积为9$\sqrt{3}$-$\frac{27}{2}$.
在正方形ABCD中,点E为BC边上的一点,连接DE,点F为DE的中点,连接FA、FB,线段FB与AC交于点G,过B作BH⊥DE交DE的延长线于点H,若BH=3,AG:GC=$\sqrt{3}$:1,则△AFG的面积为9$\sqrt{3}$-$\frac{27}{2}$.