题目内容
 如图,射线OC的解析式y=
如图,射线OC的解析式y=
| ||
| 3 |
(0,
)或(0,
)
| 1 |
| 3 |
| 4 |
| 3 |
(0,
)或(0,
)
.| 1 |
| 3 |
| 4 |
| 3 |
分析:首先根据两个函数求得点P的坐标,然后求得线段PO的长和∠AOH的度数,然后分两种情况求得点Q的坐标即可.
解答:解:∵y=
x与抛物线 y=x2交点为P,
∴
解得:x=0或x=
∵点P在第一象限,
∴x=
∴y=
×
=
∴点P的坐标为(
,
).
∴PO=
=
设A点的坐标为(a,b)
∵点A在射线OC上,
 ∴b=
∴b=
a
∴
=
=
,
∴∠AOH=30°,
①如图1,作PQ1⊥y轴,
此时△PQ1O∽△OHA
∴P点的纵坐标与Q1的纵坐标相同,
∴点Q1的坐标为(0,
);
 ②如图2,△Q2PO∽△OHA,
②如图2,△Q2PO∽△OHA,
∴∠OQ2P=∠AOH=30°,
∴OQ2P=2PO=2×
=
,
此时Q2的坐标为(0,
),
故答案为:(0,
)或(0,
)
| ||
| 3 |
∴
|
解得:x=0或x=
| ||
| 3 |
∵点P在第一象限,
∴x=
| ||
| 3 |
∴y=
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
∴点P的坐标为(
| ||
| 3 |
| 1 |
| 3 |
∴PO=
(
|
| 2 |
| 3 |
设A点的坐标为(a,b)
∵点A在射线OC上,
 ∴b=
∴b=
| ||
| 3 |
∴
| AH |
| OH |
| b |
| a |
| ||
| 3 |
∴∠AOH=30°,
①如图1,作PQ1⊥y轴,
此时△PQ1O∽△OHA
∴P点的纵坐标与Q1的纵坐标相同,
∴点Q1的坐标为(0,
| 1 |
| 3 |
 ②如图2,△Q2PO∽△OHA,
②如图2,△Q2PO∽△OHA,∴∠OQ2P=∠AOH=30°,
∴OQ2P=2PO=2×
| 2 |
| 3 |
| 4 |
| 3 |
此时Q2的坐标为(0,
| ,4 |
| 3 |
故答案为:(0,
| 1 |
| 3 |
| 4 |
| 3 |
点评:此题主要考查的是二次函数的综合知识以及函数图象交点坐标的求法;由于相似三角形的对应顶点不明确,因此要注意分类讨论思想的运用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
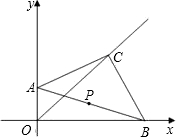 ),点B的坐标为(6,0).
),点B的坐标为(6,0).
 如图,射线OC的解析式y=
如图,射线OC的解析式y= x(x≥0),在射线OC上取一点A,过点A作AH⊥x轴于点H.设抛物线 y=x2(x>0)与射线OC的交点为P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH相似,则符合条件的点Q的坐标是________.
x(x≥0),在射线OC上取一点A,过点A作AH⊥x轴于点H.设抛物线 y=x2(x>0)与射线OC的交点为P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH相似,则符合条件的点Q的坐标是________. x(x≥0),在射线OC上取一点A,过点A作AH⊥x轴于点H.设抛物线 y=x2(x>0)与射线OC的交点为P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH相似,则符合条件的点Q的坐标是 .
x(x≥0),在射线OC上取一点A,过点A作AH⊥x轴于点H.设抛物线 y=x2(x>0)与射线OC的交点为P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH相似,则符合条件的点Q的坐标是 .