题目内容
关于x,y的二元一次方程(a-1)x+(a+2)y+5-2a=0,当a取一个确定的值时就得到一个方程,所有这些方程有一个公共解,则这个公共解是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
分析:如果当a取一个确定的值时就得到一个方程,这些方程有一个公共解,说明无论a取何值,都不影响方程,即含a的项的系数相加为0.
解答:解:方程整理为ax-x+ay+2y+5-2a=0,
a(x+y-2)-x+2y+5=0.
根据题意,即可得
,
用加减法解得
.
故选A.
a(x+y-2)-x+2y+5=0.
根据题意,即可得
|
用加减法解得
|
故选A.
点评:此题应注意思考:由于a可取任何数,要想让当a取一个确定的值时就得到一个方程,所有这些方程有一个公共解,就需让含a的项的系数相加为0,此时即可得到关于x和y的方程组.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 恋恋买了如图所示的两种奥运邮票共20枚,用去16元8角.假设左边一种邮票有x枚,右边一种有y枚,请你列出关于x,y的二元一次方程组,并写出能求解这个方程组的方法.
恋恋买了如图所示的两种奥运邮票共20枚,用去16元8角.假设左边一种邮票有x枚,右边一种有y枚,请你列出关于x,y的二元一次方程组,并写出能求解这个方程组的方法.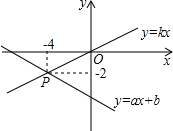 一项成绩是81分,若想学期总成绩不低于90分,则纸笔测试的成绩至少是
一项成绩是81分,若想学期总成绩不低于90分,则纸笔测试的成绩至少是