题目内容
如图，在圆O中有折线ABCO，BC=12，CO=7，∠B=∠C=60°，则AB的长为（ ）
A．17
B．18
C．19
D．20
【答案】分析：作OD⊥AB垂足为D，利用垂径定理得AB=2BD，作OE∥AB交BC于E，构造等边△COE，过E点作EF⊥AB，垂足为F，得Rt△BEF，而∠B=60°，可得BF=
BE，再根据BD=BF+DF求BD．
解答：
解：如图，作OD⊥AB垂足为D，OE∥AB交BC于E，过E点作EF⊥AB，垂足为F，
∵OE∥AB，∴△COE为等边三角形，∴OE=CE=OC=7，
∵OD⊥AB，EF⊥AB，∴DF=OE=7，BE=BC-CE=5，
在Rt△BEF中，∵∠B=60°，∴BF=
BE=
，
∴BD=BF+DF=
+7=
，
由垂径定理，得AB=2BD=19．
故选C．
点评：本题考查了垂径定理，等边三角形的性质．关键是通过作辅助线，得出等边三角形，30°的直角三角形，利用垂径定理求AB．
BE，再根据BD=BF+DF求BD．解答：
解：如图，作OD⊥AB垂足为D，OE∥AB交BC于E，过E点作EF⊥AB，垂足为F，∵OE∥AB，∴△COE为等边三角形，∴OE=CE=OC=7，
∵OD⊥AB，EF⊥AB，∴DF=OE=7，BE=BC-CE=5，
在Rt△BEF中，∵∠B=60°，∴BF=
BE=，∴BD=BF+DF=
+7=，由垂径定理，得AB=2BD=19．
故选C．
点评：本题考查了垂径定理，等边三角形的性质．关键是通过作辅助线，得出等边三角形，30°的直角三角形，利用垂径定理求AB．
练习册系列答案
相关题目
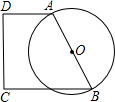如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以腰AB为直径作圆，已知AB=10，AD=M，BC=M+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则M的取值范围是（ ）| A、0≤M≤3 | B、0＜M＜3 | C、0＜M≤3 | D、3＜M＜10 |
如图，在圆O中有折线ABCO，BC=12，CO=7，∠B=∠C=60°，则AB的长为（ ）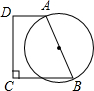
如图，在直角梯形ABCD中，AD∥BC，∠D=90°，以斜边AB为直径作圆，已知AB=10，AD=m，BC=m+4，要使圆与折线BCDA有三个公共点（A、B两点除外），则m的取值范围是
如图，在圆O中有折线ABCO，BC=12，CO=7，∠B=∠C=60°，则AB的长为