题目内容
小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到AD的距离（用含根号的式子表示）．
解：连接PA、PB，过点P作PM⊥AD于点M；延长BC，交PM于点N则∠APM=45°，∠BPM=60°，NM=10米设PM=x米
在Rt△PMA中，AM=PM×tan∠APM=xtan45°=x（米）
在Rt△PNB中，BN=PN×tan∠BPM=（x﹣10）tan60°=（x﹣10）
（米）
由AM+BN=46米，得x+（x﹣10）
=46
解得，
，
∴点P到AD的距离为
米．（结果分母有理化为
米也可）
在Rt△PMA中，AM=PM×tan∠APM=xtan45°=x（米）
在Rt△PNB中，BN=PN×tan∠BPM=（x﹣10）tan60°=（x﹣10）
（米）由AM+BN=46米，得x+（x﹣10）
=46解得，
，∴点P到AD的距离为
米．（结果分母有理化为米也可）
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
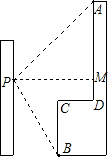（2012•资阳）小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到AD的距离（用含根号的式子表示）．
