题目内容
 如图,是双曲线
如图,是双曲线 ,
, 在第一象限内的图象,直线AB∥x轴分别交双曲线于A、B两点,则△AOB面积为
在第一象限内的图象,直线AB∥x轴分别交双曲线于A、B两点,则△AOB面积为
- A.4
- B.3
- C.2
- D.1
C
分析:根据反比例函数的几何意义,反比例函数y= 上一点P,过p作y轴的垂线PC,则△OPC的面积是
上一点P,过p作y轴的垂线PC,则△OPC的面积是 |k|,据此即可求解.
|k|,据此即可求解.
解答:∵A在反比例函数线y= 上.
上.
∴△OAC的面积是 ×2=1
×2=1
同理△OBC的面积是 ×6=3.
×6=3.
则△AOB面积为S△OBC-S△OAC=3-1=2.
故选C.
点评:本题主要考查了反比例函数的性质,正确理解三角形的面积与k的值的大小是解决本题的关键.
分析:根据反比例函数的几何意义,反比例函数y=
 上一点P,过p作y轴的垂线PC,则△OPC的面积是
上一点P,过p作y轴的垂线PC,则△OPC的面积是 |k|,据此即可求解.
|k|,据此即可求解.解答:∵A在反比例函数线y=
 上.
上.∴△OAC的面积是
 ×2=1
×2=1同理△OBC的面积是
 ×6=3.
×6=3.则△AOB面积为S△OBC-S△OAC=3-1=2.
故选C.
点评:本题主要考查了反比例函数的性质,正确理解三角形的面积与k的值的大小是解决本题的关键.

练习册系列答案
相关题目
 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线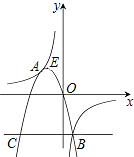 (2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线
(2012•呼和浩特)如图,抛物线y=ax2+bx+c(a<0)与双曲线
 如图,已知点A是双曲线y=
如图,已知点A是双曲线y= 在第一象限上的一动点,连接AO,以OA为一边作等腰直角三角形AOB(∠AOB=90°),点B在第四象限,随着点A的运动,点B的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为________.
在第一象限上的一动点,连接AO,以OA为一边作等腰直角三角形AOB(∠AOB=90°),点B在第四象限,随着点A的运动,点B的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为________. 如图,C,D是双曲线y=
如图,C,D是双曲线y= 在第1象限内的分支上的两点,直线CD分别交x轴、y轴于A、B两点,设C、D坐标(x1,y1),(x2,y2),连接OC、OD,求证:y1<OC<y1+
在第1象限内的分支上的两点,直线CD分别交x轴、y轴于A、B两点,设C、D坐标(x1,y1),(x2,y2),连接OC、OD,求证:y1<OC<y1+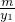 .
.