题目内容
 将等腰△ABC沿对称轴折叠,使点B与C重合,展开后得到折痕AF,再沿DE折叠,使点A与F重合,展开后得到折痕DE,则四边形ADFE是
将等腰△ABC沿对称轴折叠,使点B与C重合,展开后得到折痕AF,再沿DE折叠,使点A与F重合,展开后得到折痕DE,则四边形ADFE是
- A.平行四边形
- B.菱形
- C.矩形
- D.等腰梯形
B
分析:要证四边形AEFD是菱形,只需通过定义证明四边相等即可.此题实际是对判定菱形的方法“对角形垂直平分的四边形为菱形”的证明.
解答:∵等腰△ABC沿对称轴折叠后点B与C重合,
∴AF⊥BC
∵沿DE折叠,使点A与F重合,
∴ED∥CB
∴AF⊥DE
又∵点A与F重合,点B与C重合,
∴AF与DE互相平分,
∵AF与DE是四边形AEFD的对角线,AF与DE垂直且平分,
∴四边形AEFD是菱形.
故选B.
点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.
分析:要证四边形AEFD是菱形,只需通过定义证明四边相等即可.此题实际是对判定菱形的方法“对角形垂直平分的四边形为菱形”的证明.
解答:∵等腰△ABC沿对称轴折叠后点B与C重合,
∴AF⊥BC
∵沿DE折叠,使点A与F重合,
∴ED∥CB
∴AF⊥DE
又∵点A与F重合,点B与C重合,
∴AF与DE互相平分,
∵AF与DE是四边形AEFD的对角线,AF与DE垂直且平分,
∴四边形AEFD是菱形.
故选B.
点评:菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
相关题目
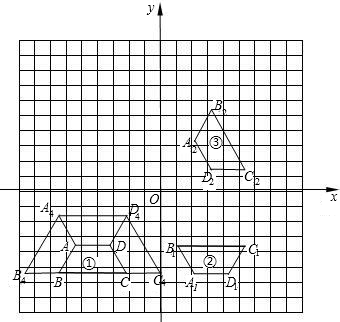 平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.
平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.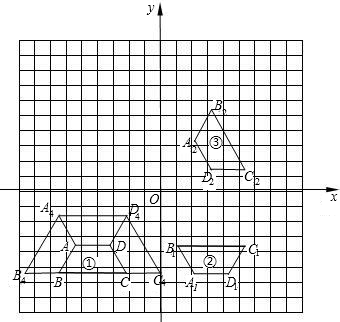 平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.
平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.

