题目内容
（2013•松北区一模）如图，四边形ABCD为梯形，AD∥BC，∠ABC=30°，∠BCD=60°，AD=4，AB=3| 3 |
分析：首先过点A作AE⊥BC于E，过点D作DF⊥BC于F，由梯形ABCD中，AD∥BC，易得四边形AEFD是矩形，可得EF=AD=4，在直角三角形ABE中利用30°角所对的直角边等于斜边的一半求出AE的长和BE的长，再在Rt△DFC中求出CF的值，从而求出BC的长．
解答：
解：过点A作AE⊥BC于E，过点D作DF⊥BC于F，
∵AD∥BC，
∴四边形AEFD是矩形，
∴EF=AD=4，
∵∠ABC=30°，AB=3
，
∴AE=
AB=
，
∴BE=
=
∴AE=DF=
，
在Rt△DFC中，tan60°=
=
，
∴CF=
=
，
∴BC=BE+EF+CF=
+4+
=10，
故选C．
解：过点A作AE⊥BC于E，过点D作DF⊥BC于F，∵AD∥BC，
∴四边形AEFD是矩形，
∴EF=AD=4，
∵∠ABC=30°，AB=3
| 3 |
∴AE=
| 1 |
| 2 |
3
| ||
| 2 |
∴BE=
| AB 2-AE2 |
| 9 |
| 2 |
∴AE=DF=
3
| ||
| 2 |
在Rt△DFC中，tan60°=
| DF |
| FC |
| 3 |
∴CF=
| ||||
|
| 3 |
| 2 |
∴BC=BE+EF+CF=
| 9 |
| 2 |
| 3 |
| 2 |
故选C．
点评：此题考查了梯形的性质，直角三角形的性质以及三角函数的应用．此题难度不大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．
练习册系列答案
阅读快车系列答案
相关题目
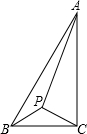（2013•松北区一模）如图，P为△ABC内一点，∠BAC=30°，∠ACB=90°，∠BPC=120°．若BP=