Ő‚ńŅńŕ»›
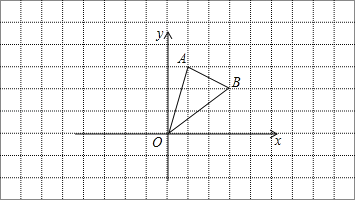
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ķ»—Ł÷ĪĹ«»żĹ«–őOABĶń»żłŲ∂®Ķ„∑÷Īūő™![]() °Ę
°Ę![]() °Ę
°Ę![]() £¨ĻżA◊ųy÷ŠĶńīĻŌŖ
£¨ĻżA◊ųy÷ŠĶńīĻŌŖ![]() .Ķ„C‘ŕx÷Š…Ō“‘√Ņ√Ž
.Ķ„C‘ŕx÷Š…Ō“‘√Ņ√Ž![]() ĶńňŔ∂»ī”‘≠Ķ„≥Ų∑ĘŌÚ”“‘ň∂Į£¨Ķ„D‘ŕ
ĶńňŔ∂»ī”‘≠Ķ„≥Ų∑ĘŌÚ”“‘ň∂Į£¨Ķ„D‘ŕ![]() …Ō“‘√Ņ√Ž
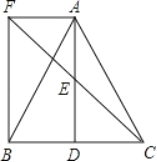
…Ō“‘√Ņ√Ž![]() ĶńňŔ∂»Õ¨ Īī”Ķ„A≥Ų∑ĘŌÚ”“‘ň∂Į£¨ĶĪňńĪŖ–őABCDő™∆Ĺ––ňńĪŖ–ő ĪC°ĘDÕ¨ ĪÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™
ĶńňŔ∂»Õ¨ Īī”Ķ„A≥Ų∑ĘŌÚ”“‘ň∂Į£¨ĶĪňńĪŖ–őABCDő™∆Ĺ––ňńĪŖ–ő ĪC°ĘDÕ¨ ĪÕ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™![]() .ĶĪC°ĘDÕ£÷Ļ‘ň∂Į Ī£¨Ĺę°ųOAB—ōy÷ŠŌÚ”“∑≠’ŘĶ√ĶĹ°ų
.ĶĪC°ĘDÕ£÷Ļ‘ň∂Į Ī£¨Ĺę°ųOAB—ōy÷ŠŌÚ”“∑≠’ŘĶ√ĶĹ°ų![]() £¨
£¨![]() ”ŽCDŌŗĹĽ”ŕĶ„E£¨Pő™x÷Š…ŌŃŪ“Ľ∂ĮĶ„.
”ŽCDŌŗĹĽ”ŕĶ„E£¨Pő™x÷Š…ŌŃŪ“Ľ∂ĮĶ„.
(1)«ů÷ĪŌŖABĶńĹ‚őŲ Ĺ£¨≤Ę«ů≥ŲtĶń÷Ķ.
(2)ĶĪPE+PD»°Ķ√◊Ó–°÷Ķ Ī£¨«ů![]() Ķń÷Ķ.
Ķń÷Ķ.
(3)…ŤPĶń‘ň∂ĮňŔ∂»ő™1£¨»ŰPī”BĶ„≥Ų∑ĘŌÚ”“‘ň∂Į£¨‘ň∂Į Īľšő™![]() £¨«Ž”√ļ¨
£¨«Ž”√ļ¨![]() Ķńīķ ż ĹĪŪ ĺ°ųPAEĶń√śĽż.
Ķńīķ ż ĹĪŪ ĺ°ųPAEĶń√śĽż.

°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©
£Ľ£®2£©![]() £Ľ (3)ĘŔĶĪ
£Ľ (3)ĘŔĶĪ![]() Ī£¨S°ųPAE=
Ī£¨S°ųPAE=![]() ,ĘŕĶĪ
,ĘŕĶĪ![]() Ī, S°ųPAE=
Ī, S°ųPAE=![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©…Ť÷ĪŌŖABő™![]() £¨į—B(-3,0)īķ»Ž£¨«ůĶ√k£¨»∑∂®Ĺ‚őŲ Ĺ£Ľ‘Ŕ…Ť…Ť
£¨į—B(-3,0)īķ»Ž£¨«ůĶ√k£¨»∑∂®Ĺ‚őŲ Ĺ£Ľ‘Ŕ…Ť…Ť![]() √ŽļůĻĻ≥…∆Ĺ––ňńĪŖ–ő£¨łýĺ›Ő‚“‚Ń–≥Ų∑Ĺ≥Ő£¨«ů≥ŲtľīŅ…£Ľ
√ŽļůĻĻ≥…∆Ĺ––ňńĪŖ–ő£¨łýĺ›Ő‚“‚Ń–≥Ų∑Ĺ≥Ő£¨«ů≥ŲtľīŅ…£Ľ
£®2£©ĻżE◊ųĻō”ŕ![]() ÷Š∂‘”ŕĶ„
÷Š∂‘”ŕĶ„![]() ,ѨŔEE°šĹĽx÷Š”ŕĶ„P,‘Úīň ĪPE+PD◊Ó–°.”…£®1£©Ķ√ĶĹĶĪt=2 Ī£¨”–C£®
,ѨŔEE°šĹĽx÷Š”ŕĶ„P,‘Úīň ĪPE+PD◊Ó–°.”…£®1£©Ķ√ĶĹĶĪt=2 Ī£¨”–C£®![]() £¨0£©£¨D(
£¨0£©£¨D(![]() ,3)£¨‘Ŕłýĺ›AB°őCD£¨«ů≥Ų÷ĪŌŖCDļÕAB1ĶńĹ‚őŲ Ĺ£¨»∑∂®EĶń◊ÝĪÍ£Ľ»Ľļů‘ŔÕ®Ļż≥ň∑®Ļę ĹļÕŌŖ∂ő‘ňň„£¨ľīŅ…ÕÍ≥…Ĺ‚īū.
,3)£¨‘Ŕłýĺ›AB°őCD£¨«ů≥Ų÷ĪŌŖCDļÕAB1ĶńĹ‚őŲ Ĺ£¨»∑∂®EĶń◊ÝĪÍ£Ľ»Ľļů‘ŔÕ®Ļż≥ň∑®Ļę ĹļÕŌŖ∂ő‘ňň„£¨ľīŅ…ÕÍ≥…Ĺ‚īū.
£®3£©łýĺ›£®1£©Ņ…“‘Ň–∂Ō”–![]() ļÕ
ļÕ![]() ŃĹ÷÷«ťŅŲ£¨»Ľļů∑÷ņŗŐ÷¬ŘľīŅ….
ŃĹ÷÷«ťŅŲ£¨»Ľļů∑÷ņŗŐ÷¬ŘľīŅ….
£®1£©Ĺ‚£ļ…Ť÷ĪŌŖABő™![]() £¨į—B(-3,0)īķ»ŽĶ√£ļ
£¨į—B(-3,0)īķ»ŽĶ√£ļ
![]()
°ŗ![]()
°ŗ![]()
”…Ő‚“‚Ķ√£ļ
…Ť![]() √ŽļůĻĻ≥…∆Ĺ––ňńĪŖ–ő£¨‘Ú
√ŽļůĻĻ≥…∆Ĺ––ňńĪŖ–ő£¨‘Ú
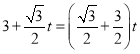
Ĺ‚÷ģĶ√£ļ![]() £¨
£¨
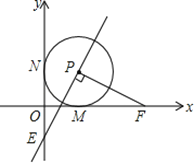
£®2£©»ÁÕľ:ĻżE◊ųĻō”ŕ![]() ÷Š∂‘”ŕĶ„
÷Š∂‘”ŕĶ„![]() ,
,
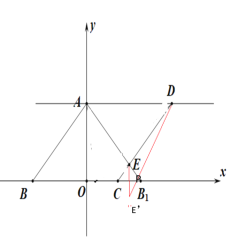
ѨŔEE°šĹĽx÷Š”ŕĶ„P,‘Úīň ĪPE+PD◊Ó–°.
”…£®1£©t=2Ķ√£ļ
°ŗC£®![]() £¨0£©£¨D(
£¨0£©£¨D(![]() ,3)
,3)
°ŖAB°őCD
°ŗ…ŤCDő™![]()
į—C£®![]() £¨0£©īķ»ŽĶ√
£¨0£©īķ»ŽĶ√
b1=![]()
°ŗCDő™£ļ![]()
“◊Ķ√![]() ő™£ļ
ő™£ļ![]()
°ŗ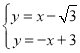
Ĺ‚÷ģĶ√£ļE(![]() ,
,![]() )
)
°ŗ
(3)ĘŔĶĪ![]() Ī
Ī
S°ųPAE=S°ųPAB1-S°ųPEB1=
![]()
ĘŕĶĪ![]() Ī£ļ
Ī£ļ
S°ųPAE=S°ųPAB1-S°ųPEB1=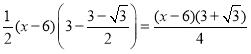

°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ĺę“Ľ’Ň’ż∑Ĺ–ő÷Ĺ∆¨£¨ľŰ≥…ňńłŲīů–°–ő◊ī“Ľ—ýĶń–°’ż∑Ĺ–ő£¨»ĽļůĹę∆š÷–Ķń“ĽłŲ–°’ż∑Ĺ–ő‘ŔįīÕ¨—ýĶń∑Ĺ∑®ľŰ≥…ňńłŲ–°’ż∑Ĺ–ő£¨‘ŔĹę∆š÷–Ķń“ĽłŲ–°’ż∑Ĺ–őľŰ≥…ňńłŲ–°’ż∑Ĺ–ő£¨»Áīň—≠Ľ∑ĹÝ––Ō¬»•£Ľ

£®1£©ŐÓĪŪ£ļ
ľŰĶńīő ż | 1 | 2 | 3 | 4 | 5 |
’ż∑Ĺ–őłŲ ż |
£®2£©»ÁĻŻľŰnīő£¨Ļ≤ľŰ≥Ų∂ŗ…ŔłŲ–°’ż∑Ĺ–ő£Ņ
£®3£©»ÁĻŻľŰŃň100īő£¨Ļ≤ľŰ≥Ų∂ŗ…ŔłŲ–°’ż∑Ĺ–ő£Ņ
£®4£©ĻŘ≤žÕľ–ő£¨ľŰŃňnīő£¨–°’ż∑Ĺ–őĶńĪŖ≥§ő™‘≠ņīĶń £¨√śĽż «‘≠ņīĶń .