题目内容
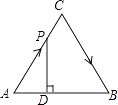
【题目】如图, 直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,点
,点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点, 点
的中点, 点![]() 为
为![]() 上一动点, 当
上一动点, 当![]() 最小时, 点
最小时, 点![]() 的坐标为
的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】
(方法一)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
(方法二)根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,根据三角形中位线定理即可得出点P为线段CD′的中点,由此即可得出点P的坐标.
解:(方法一)如图所示
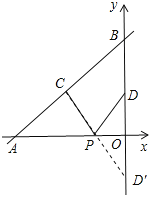
作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=-6,
x+4=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(-3,2),D′(0,-2),
∴有![]() ,解得:
,解得: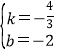 ,
,
∴直线CD′的解析式为y=![]() ,
,
令y=![]() 中y=0,则0=
中y=0,则0=![]() 解得:x=
解得:x=![]() ,
,
∴点P的坐标为![]() .
.
故选C.
(方法二)如图所示
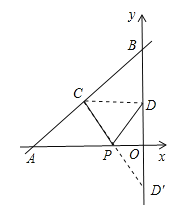
连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,
令y=![]() 中x=0,则y=4,
中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() 中y=0,则
中y=0,则![]() =0,解得:x=-6,
=0,解得:x=-6,
∴点A的坐标为(-6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(-3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,-2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(![]() ).
).
故选:C.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个
B.3个
C.2个
D.1个