题目内容
已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC∥AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法种数共有
- A.6种
- B.5种
- C.4种
- D.3种
C
分析:根据平行四边形的判定方法即可找到所有组合方式:(1)两组对边平行①③;(2)两组对边相等②④;(3)一组对边平行且相等①②或③④,所以有四种组合.
解答:依题意得有四种组合方式:
(1)①③,利用两组对边平行的四边形是平行四边形判定;
(2)②④,利用两组对边相等的四边形是平行四边形判定;
(3)①②或③④,利用一组对边平行且相等的四边形是平行四边形判定.
故选C.
点评:此题主要考查了平行四边形的判定方法,熟练掌握平行四边形的判定方法是解题的关键.
分析:根据平行四边形的判定方法即可找到所有组合方式:(1)两组对边平行①③;(2)两组对边相等②④;(3)一组对边平行且相等①②或③④,所以有四种组合.
解答:依题意得有四种组合方式:
(1)①③,利用两组对边平行的四边形是平行四边形判定;
(2)②④,利用两组对边相等的四边形是平行四边形判定;
(3)①②或③④,利用一组对边平行且相等的四边形是平行四边形判定.
故选C.
点评:此题主要考查了平行四边形的判定方法,熟练掌握平行四边形的判定方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
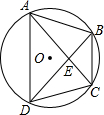 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |
如图,已知四边形ABCD是边长为2的正方形,E是AB的中点,F是BC的中点,AF与DE相交于G,BD和AF相交于H,那么四边形BEGH的面积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
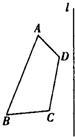 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.