题目内容
如图，AB为⊙O的弦，半径OC⊥AB于点D，若OB长为10，cos∠BOD=
，则AB的长是（ ）
A．20
B．16
C．12
D．8
【答案】分析：首先根据三角函数cos∠BOD=
算出DO的长，再利用勾股定理算出BD的长，再根据平分弦（不是直径）的直径垂直于弦，并且平分弦可得到AB的长．
解答：解：∵cos∠BOD=
，
∴
=
，
∵BO=10，
∴DO=6，
∵OC⊥AB，
∴∠ODB=90°，
在Rt△BOD中，BD=
=
=8，
∴AB=2DB=16，
故选：B．
点评：此题主要考查了垂径定理的应用，以及勾股定理的应用，关键是利用勾股定理计算出DB的长．
算出DO的长，再利用勾股定理算出BD的长，再根据平分弦（不是直径）的直径垂直于弦，并且平分弦可得到AB的长．解答：解：∵cos∠BOD=
，∴
=，∵BO=10，
∴DO=6，
∵OC⊥AB，
∴∠ODB=90°，
在Rt△BOD中，BD=
==8，∴AB=2DB=16，
故选：B．
点评：此题主要考查了垂径定理的应用，以及勾股定理的应用，关键是利用勾股定理计算出DB的长．
练习册系列答案
名校课堂系列答案
相关题目
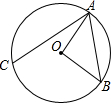如图，AB为⊙O的弦，∠AOB=100°，点C在⊙O上，且 
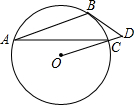已知：如图，AB为⊙O的弦，过点O作AB的平行线，交⊙O于点C，直线OC上一点D满足∠D=∠ACB．
54、如图，AB为⊙O的弦，C、D为直线AB上两点，要使OC=OD，则图中的线段必满足的条件是
（2012•闵行区三模）已知：如图，AB为⊙O的弦，OD⊥AB，垂足为点D，DO的延长线交⊙O于点C．过点C作CE⊥AO，分别与AB、AO的延长线相交于E、F两点．CD=8，sin∠A=
如图，AB为⊙0的弦，⊙0的半径为10，0C⊥AB于点D，交⊙0于点C，且CD=2，则弦AB的长是