题目内容
如图,点A(2,-1)是抛物线y=ax2+bx+c上一点,则不等式ax2+bx+c<- x+
x+ <0的解集为________
<0的解集为________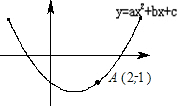
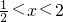
分析:先求出函数y=-
 x+
x+ 与x轴的交点坐标为(
与x轴的交点坐标为( ,0),并且A(2,-1)在其图象上,再画出它的图象,然后观察图象即可得到满足不等式ax2+bx+c<-
,0),并且A(2,-1)在其图象上,再画出它的图象,然后观察图象即可得到满足不等式ax2+bx+c<- x+
x+ <0的对应的x的范围.
<0的对应的x的范围.解答:对于函数y=-
 x+
x+ ,
,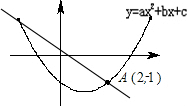
令y=0,则-
 x+
x+ =0,解得x=
=0,解得x= ,即函数y=-
,即函数y=- x+
x+ 与x轴的交点坐标为(
与x轴的交点坐标为( ,0),
,0),并且A(2,-1)在其图象上,如图,
∵ax2+bx+c<-
 x+
x+ <0,即函数值都小于0,并且抛物线y=ax2+bx+c的函数值要比一次函数y=-
<0,即函数值都小于0,并且抛物线y=ax2+bx+c的函数值要比一次函数y=- x+
x+ 的值小,
的值小,观察图象可得,
 <x<2.
<x<2.∴不等式ax2+bx+c<-
 x+
x+ <0的解集为
<0的解集为 <x<2.
<x<2.故答案为
 <x<2.
<x<2.点评:本题考查了利用二次函数的图象与一次函数的图象解不等式:先要画出两函数的图象,并且得到它们的交点坐标,然后根据图象的位置的高低确定对应的自变量的取值范围.

练习册系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是