Question

【题目】如图，在中，，，，分别是，，的对边，点是上一个动点（点与、不重合），连，若、满足，且是不等式组的最大整数解.

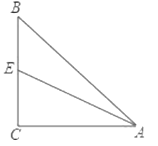
（1）求，，的长；

（2）若平分的周长，求的大小；

（3）是否存在线段将三角形的周长和面积同时平分？若存在，求出的长；若不存在，请说明理由.

Answer 1

【答案】（1），，；（2）；（3）不存在.理由见解析.

【解析】

（1）根据二元一次方程组的解法得出a，b的值，再利用不等式组的解法得出x的取值范围，进而得出c的值；
（2）利用（1）中所求以及等腰直角三角形的性质得出AC=CE，进而得出答案；
（3）分别根据AE平分三角形ABC的周长和平分面积时不能同时符合要求进而得出答案．

（1）解方程组，

得：，

解不等式组，

解得：，

∵满足的最大正整数为10，

∴，∴，，；

（2）∵平分的周长，的周长为24，

∴，

∴，，

∴，

∴为等腰直角三角形，

∴，；

（3）不存在.

∵当将分成周长相等的和时，，，

此时，的面积为：，

的面积为：面积不相等，

∴平分的周长时，不能平分的面积，

同理可说明平分的面积时，不能平分的周长.