题目内容
如图，在边长为单位1的网络中，先将线段AB沿一确定的方向平移得到线段CD．点A的对应点为C，点B的对应点D的位置如图，再将线段CD绕O顺时针旋转90°得到线段EF，点C的对应点为E（1）画出线段CD，EF；
（2）直接写出在这两次变换过程中，点A经过C到达E的路径长．
分析：（1）根据网格结构找出点C，然后连接即可得到线段CD，再找出点C、D绕点O顺时针旋转90°后的对应点EF，然后连接即可得解；
（2）根据勾股定理列式求出AC、OC，利用弧长公式求出点C到E的弧长，然后相加即可得解．
（2）根据勾股定理列式求出AC、OC，利用弧长公式求出点C到E的弧长，然后相加即可得解．
解答：解答：（1）线段CD，EF如图所示；
（2）根据勾股定理，AC=
=
，
OC=
=5，
C到E的路径长为
=
π，
所以，点A经过C到达E的路径长为：
+
π．
（2）根据勾股定理，AC=
| 12+42 |
| 17 |
OC=
| 32+42 |
C到E的路径长为
| 90•π•5 |
| 180 |
| 5 |
| 2 |
所以，点A经过C到达E的路径长为：
| 17 |
| 5 |
| 2 |
点评：本题考查了利用旋转变换作图，弧长的计算，熟练掌握网格结构是解题的关键．
练习册系列答案
相关题目
20、作图题：（不要求写作法）如图，在边长为单位1的正方形网格中，有一个格点△ABC（各个顶点都是正方形网格的格点）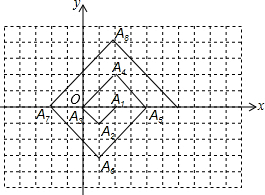
如图，在边长为单位1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，都是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，-1），A3（0，0），则依图中所示规律，顶点A2014的坐标为
如图，在边长为单位1的网络中，先将线段AB沿一确定的方向平移得到线段CD．点A的对应点为C，点B的对应点D的位置如图，再将线段CD绕O顺时针旋转90°得到线段EF，点C的对应点为E