题目内容
 (2010•贺州)如图,在梯形ABCD中,AD∥BC,AC、BD是梯形的对角线,且AC⊥BD,AD=3cm,BC=7cm,BD=6cm,则梯形ABCD的面积是
(2010•贺州)如图,在梯形ABCD中,AD∥BC,AC、BD是梯形的对角线,且AC⊥BD,AD=3cm,BC=7cm,BD=6cm,则梯形ABCD的面积是24
24
cm2.分析:过D作DE∥AC,交BC延长线于E,过D作DF⊥BE于F,首先证明四边形ADEC是平行四边形,根据平行四边形对边相等可得到CE=AD,进而可算出BE的长,再利用勾股定理算出DE的长,根据三角形的面积公式可以计算出梯形的高DF的长,最后利用梯形的面积公式可以计算出梯形ABCD面积.
解答:解:过D作DE∥AC,交BC延长线于E,过D作DF⊥BE于F,
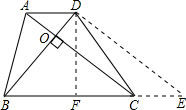
则四边形ADEC是平行四边形,
从而可得:AD=CE=3cm,
故可得:BE=3+7=10cm,
∵AC⊥BD,
∴∠BDE=90°,
∵AC∥DE,
∴∠BDE=90°,
在Rt△BDE中,DE=
=
=8cm,
故S△BDE=
×DB×DE=
×6×8=24,
即可得
×DF×BE=24,
解得:DF=
cm,
从而可得梯形ABCD面积为:
(AD+BC)×DF=
×10×
=24cm2.
故答案为:24.

则四边形ADEC是平行四边形,
从而可得:AD=CE=3cm,
故可得:BE=3+7=10cm,
∵AC⊥BD,
∴∠BDE=90°,
∵AC∥DE,
∴∠BDE=90°,
在Rt△BDE中,DE=
| BE2-BD2 |
| 100-36 |
故S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
即可得
| 1 |
| 2 |
解得:DF=
| 24 |
| 5 |
从而可得梯形ABCD面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
故答案为:24.
点评:此题主要考查了梯形的面积计算,三角形的面积计算,以及平行四边形的判定与性质,关键是求出梯形的高DF的长度.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
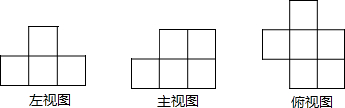 (2010•贺州)如图是由一些大小相同的小正方体搭成的一个几何体的三视图,则这个几何体的小正方体个数共有( )
(2010•贺州)如图是由一些大小相同的小正方体搭成的一个几何体的三视图,则这个几何体的小正方体个数共有( )
 (2010•贺州)如图,△NKM与△ABC是两块完全相同的45°的三角尺,将△NKM的直角顶点M放在△ABC的斜边AB的中点处,且MK经过点C,设AC=a.则两个三角尺的重叠部分△ACM的周长是
(2010•贺州)如图,△NKM与△ABC是两块完全相同的45°的三角尺,将△NKM的直角顶点M放在△ABC的斜边AB的中点处,且MK经过点C,设AC=a.则两个三角尺的重叠部分△ACM的周长是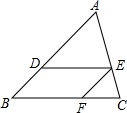 (2010•贺州)如图,在△ABC中,DE∥BC,EF∥AB.
(2010•贺州)如图,在△ABC中,DE∥BC,EF∥AB.