题目内容
 如图,已知A、B两点的坐标分别为(4,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,反比例函数图象
如图,已知A、B两点的坐标分别为(4,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,反比例函数图象 经过点P,则k的值为________.
经过点P,则k的值为________.
9
分析:连接BP,AP,利用勾股定理在Rt△ABO中求出AB2=BO2+OA2=4+16=20,再证明BP=PA,过P作PD⊥OA,在Rt△ABP中,首先求出OD=DP,再利用勾股定理求出DP的长,进而求出P点坐标,再利用待定系数法求出反比例函数关系式中的k.
解答: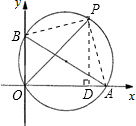 解:连接BP,AP,
解:连接BP,AP,
在Rt△ABO中,
AB2=BO2+OA2,
∵A、B两点的坐标分别为(4,0)、(0,2),
∴OA=4,OB=2,
∴AB2=BO2+OA2=4+16=20,
∵∠AOP=45°,
∴∠PBA=45°,
∵∠BPA=90°,
∴∠PAB=45°,
∴BP=PA,
在Rt△ABP中,
AB2=BP2+PA2,
∴BP=AP= ,
,
过P作PD⊥OA,
∵∠AOP=45°,
∴∠OPD=45°,
∴PD=OD,
设OD=DP=x,则AD=4-x,
在Rt△ADP中,
AP2=DP2+DA2,
∴10=x2+(4-x)2,
解得:x=1(不合题意,舍去)或3,
∴P(3,3)
∵反比例函数图象 经过点P
经过点P
∴k=3×3=9,
故答案为:9.
点评:此题主要考查了勾股定理,圆周角定理,与待定系数法求反比例函数关系式,是一个综合题,正确作出辅助线,求出P点坐标是做题的关键.
分析:连接BP,AP,利用勾股定理在Rt△ABO中求出AB2=BO2+OA2=4+16=20,再证明BP=PA,过P作PD⊥OA,在Rt△ABP中,首先求出OD=DP,再利用勾股定理求出DP的长,进而求出P点坐标,再利用待定系数法求出反比例函数关系式中的k.
解答:
 解:连接BP,AP,
解:连接BP,AP,在Rt△ABO中,
AB2=BO2+OA2,
∵A、B两点的坐标分别为(4,0)、(0,2),
∴OA=4,OB=2,
∴AB2=BO2+OA2=4+16=20,
∵∠AOP=45°,
∴∠PBA=45°,
∵∠BPA=90°,
∴∠PAB=45°,
∴BP=PA,
在Rt△ABP中,
AB2=BP2+PA2,
∴BP=AP=
 ,
,过P作PD⊥OA,
∵∠AOP=45°,
∴∠OPD=45°,
∴PD=OD,
设OD=DP=x,则AD=4-x,
在Rt△ADP中,
AP2=DP2+DA2,
∴10=x2+(4-x)2,
解得:x=1(不合题意,舍去)或3,
∴P(3,3)
∵反比例函数图象
 经过点P
经过点P∴k=3×3=9,
故答案为:9.
点评:此题主要考查了勾股定理,圆周角定理,与待定系数法求反比例函数关系式,是一个综合题,正确作出辅助线,求出P点坐标是做题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
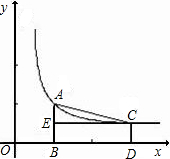 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(
如图,已知A、B两点的坐标分别为( 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论. 如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.
如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.