题目内容
定义T0(x0,y0)是双曲线 上一点,如果满足x0=y0,则称T0为双曲线
上一点,如果满足x0=y0,则称T0为双曲线 的拐点.已知双曲线
的拐点.已知双曲线 的拐点T1与抛物线y=x2-tx+t的顶点T2的连线经过原点,求t的值.
的拐点T1与抛物线y=x2-tx+t的顶点T2的连线经过原点,求t的值.
解:若双曲线 存在拐点,则有t>0,
存在拐点,则有t>0,
根据拐点的定义可得:双曲线 的拐点为:(
的拐点为:( ,
, ),(-
),(- ,-
,- ),
),
抛物线y=x2-tx+t的顶点T2的坐标为:( ,t-
,t-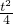 ),
),
拐点T1与顶点T2的连线的经过原点,故其解析式为:y=x,
将抛物线的顶点代入上述解析式得:t-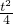 =
= ,
,
解得:t=2或0(舍去).
故t的值为2.
分析:根据题意若双曲线 存在拐点,则有t>0,求出双曲线的拐点和抛物线的顶点,再根据它们的连线经过原点,即可求出t的值.
存在拐点,则有t>0,求出双曲线的拐点和抛物线的顶点,再根据它们的连线经过原点,即可求出t的值.
点评:本题考查了二次函数的问题,难度不大,注意准确求出拐点和顶点坐标是关键.
 存在拐点,则有t>0,
存在拐点,则有t>0,根据拐点的定义可得:双曲线
 的拐点为:(
的拐点为:( ,
, ),(-
),(- ,-
,- ),
),抛物线y=x2-tx+t的顶点T2的坐标为:(
 ,t-
,t-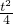 ),
),拐点T1与顶点T2的连线的经过原点,故其解析式为:y=x,
将抛物线的顶点代入上述解析式得:t-
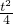 =
= ,
,解得:t=2或0(舍去).
故t的值为2.
分析:根据题意若双曲线
 存在拐点,则有t>0,求出双曲线的拐点和抛物线的顶点,再根据它们的连线经过原点,即可求出t的值.
存在拐点,则有t>0,求出双曲线的拐点和抛物线的顶点,再根据它们的连线经过原点,即可求出t的值.点评:本题考查了二次函数的问题,难度不大,注意准确求出拐点和顶点坐标是关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目