��Ŀ����
����Ŀ����֪��P��һ�κ���y=kx+b��k��bΪ��������k��0��b��0����ͼ���ϣ�����P����ƽ��1����λ��������ƽ��2����λ�õ���Q����QҲ�ڸú���y=kx+b��ͼ���ϣ�
��1��k��ֵ����
��2����ͼ����һ�κ�����ͼ��ֱ���x�ᡢy�ύ��A��B���㣬���뷴��������y= ![]() ͼ����C��D���㣨��C�ڵڶ������ڣ�������C��CE��x���ڵ�E����S1Ϊ�ı���CEOB�������S2Ϊ��OAB���������
ͼ����C��D���㣨��C�ڵڶ������ڣ�������C��CE��x���ڵ�E����S1Ϊ�ı���CEOB�������S2Ϊ��OAB��������� ![]() =
= ![]() ����b��ֵ�� ��
����b��ֵ�� �� 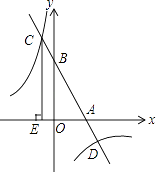
���𰸡�
��1����2
��2��3 ![]()
���������⣺��1�����P������Ϊ��m��n�������Q������Ϊ��m��1��n+2����
������ã� ![]() ��
��
��ã�k=��2��
���Դ��ǣ���2��
��2����BO��x�ᣬCE��x�ᣬ
��BO��CE��
���AOB�ס�AEC��
�֡� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
��һ�κ���y=��2x+b��x=0����y=b��
��BO=b��
��һ�κ���y=��2x+b��y=0����0=��2x+b��
��ã�x= ![]() ����AO=
����AO= ![]() ��
��
�ߡ�AOB�ס�AEC���� ![]() =
= ![]() ��
��
�� ![]() ��
��
��AE= ![]() AO=
AO= ![]() b��CE=
b��CE= ![]() BO=
BO= ![]() b��OE=AE��AO=
b��OE=AE��AO= ![]() b��
b��
��OECE=|��4|=4���� ![]() b2=4��
b2=4��
��ã�b=3 ![]() ����b=��3
����b=��3 ![]() ����ȥ����
����ȥ����
���Դ��ǣ�3 ![]() ��
��
�����㾫�����������⣬������Ҫ�˽����ϵ��k�ļ�������(�������壺��ʾ����������ͼ���ϵĵ����������������Ĵ��߶�����������Χ�ɵľ��ε����)����Ҫ����ƽ���ߵ��ж�(ͬλ����ȣ���ֱ��ƽ��;�ڴ�����ȣ���ֱ��ƽ��;ͬ���ڽǻ�������ֱ��ƽ��)�����֪ʶ���Ǵ���Ĺؼ���