Question

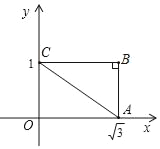
【题目】如图，在Rt△ABC中，∠B＝90°，∠ACB＝30°，其直角边分别与坐标轴垂直，已知顶点的坐标为A（，0），C（0，1）．

（1）如果A关于BC对称的点是D，则点D的坐标为　 　；

（2）过点B作直线m∥AC，交CD连线于E，求△BCE的面积．

Answer 1

【答案】（1）点D（，2），（2）S△BCE=．

【解析】

（1）由轴对称的定义得AB=BD=OC=1，据此即可得出答案；

（2）由AB=BD且BE∥AC知BE是△ACD的中位线，据此可得△BDE∽△ADC及，先求得S△ADC=、S△BDE=，再根据S△BCE=S△ADC-S△BDE-S△ABC可得答案．

（1）如图，

∵A关于BC对称的点是D，

∴AB=BD=OC=1，

∴点D（，2），

（2）∵AB=BD且BE∥AC，

∴BE是△ACD的中位线，

则△BDE∽△ADC，

∴，

∵S△ADC=×2×=，

∴S△BDE=，

则S△BCE=S△ADC-S△BDE-S△ABC=--××1=．