题目内容

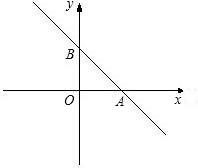如图：直线y=-x+6与坐标轴分别相交于点A、B，点P是直线AB上的一点，Q是双曲线 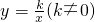$数学公式$ 上的一点，若O、A、P、Q为顶点的四边形是菱形，请在图中找出所有符合条件的点Q，并求出点Q的坐标和写出相应k的值．

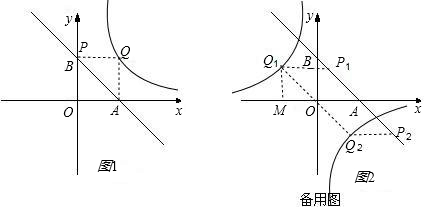
解：令y=0得x=6，令x=0得y=6，可加A，B两点坐标分别为：A（6，0），B（0，6）；此处利用到课本关于坐标x轴上的点纵坐标为零，y轴上的点横坐标为零；
∵P在AB上，
∴P在直线y=-x+6上，这样可设P点坐标为（x，-x+6）；这种设未知数简便了运算；
（1）根据OQAP为菱形，则|OP|=|AP|，（菱形四个边相等的性质）；
由两点距离公式得：|OP|= $\text{[math]}$ = $\text{[math]}$ ，
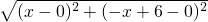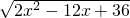|AP|= $\text{[math]}$ = $\text{[math]}$ ；
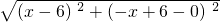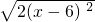∴2x²-12x+36=2（x-6）²，
解得：x=3；
于是点P的坐标为：（3，3）；
设Q坐标（xq，yq）又由于OA的中点坐标为：（3，0）；PQ的中点的坐标为：（ $\text{[math]}$ ， $\text{[math]}$ ），
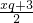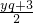根据菱形的性质OQ的中点即为PA的中点，
∴3= 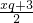$\text{[math]}$ ，0= $\text{[math]}$ ，
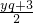解得：x_q=3，y_q=-3
∴此时点Q坐标为：（3，-3），k=3×（-3）=-9；

（2）同理，OAQP为菱形时，|OA|=|OP|
$\text{[math]}$ = $\text{[math]}$ ，
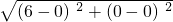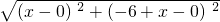解得：x=0或x=6；
P点坐标为（0，6）或（6，0）（当P点为（6，0）与A点重合，无法组成菱形PAQP所以舍去）
此时：O（0，0）A（6，0）Q（xq，yq）P（0，6）
OQ中点即为AP中点有：x_q=6，y_q=6，
Q点坐标为：（6，6），k=6×6=36；

（3）同理，OAPQ为菱形时，|OP|=|AP|
$\text{[math]}$ = $\text{[math]}$ ，
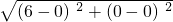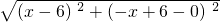解得x=6+3 $\text{[math]}$ 或x=6-3 $\text{[math]}$ ；
P点坐标为：（6+3 $\text{[math]}$ ，-3 $\text{[math]}$ ）或（6-3 $\text{[math]}$ ，3 $\text{[math]}$ ）
此时O（0，0），A（6，0），P（6+3 $\text{[math]}$ ，-3 $\text{[math]}$ ）或（6-3 $\text{[math]}$ ，3 $\text{[math]}$ ），Q（xq，yq）
OP中点即为AQ中点，可以求出：
Q点坐标为：（3 $\text{[math]}$ ，-3 $\text{[math]}$ ）或（-3 $\text{[math]}$ ，3 $\text{[math]}$ ），k=3 $\text{[math]}$ ×（-3 $\text{[math]}$ ）=（-3 $\text{[math]}$ ）×3 $\text{[math]}$ =-18；
分析：当双曲线 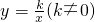$\text{[math]}$ 在一、三象限时，P、B两点重合，Q点为正方形BOAQ的一个顶点，图形符合题意；
当双曲线 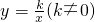$\text{[math]}$ 在二、四象限时，作OQ∥AB，且OQ=OA=6，再作PQ∥OA交直线AB于P点，图形符合题意．
点评：理解菱形的四边相等，对边平行，是判断本题的关键，需要根据双曲线所在的象限分类解题，明确正方形属于菱形的特殊情况．