题目内容
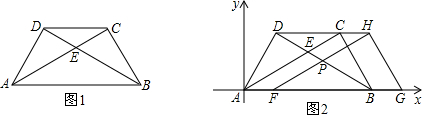
如图1,若四边形ABCD、四边形CFED都是正方形,显然图中有AG=CE,AG⊥CE.
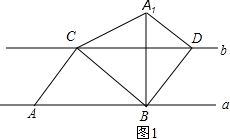
⑴当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明;若不成立,请说明理由.
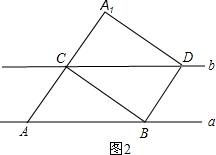
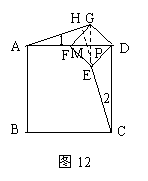
⑵当正方形GFED绕D旋转到如图3的位置时(点F在AD上),延长CE交AG于H,交AD于M.
①求证:AG⊥CH;②当AD=4,DG=![]() 时,求CH的长.
时,求CH的长.

解:(1)![]() 成立.
成立.
![]() 四边形
四边形![]() 、四边形
、四边形![]() 是正方形,
是正方形,
∴![]()
 ∠
∠![]() ∠
∠![]() .
.
∴∠![]() 90°-∠
90°-∠![]() ∠
∠![]()
∴△![]() △
△![]() .
.
∴![]() . ……………3分
. ……………3分
(2)①类似(1)可得△![]() △
△![]() ,
,
∴∠1=∠2 又∵∠![]() =∠
=∠![]() .
.
∴∠![]() ∠
∠![]() =
=![]() 即
即![]()
②过![]() 作
作![]() 于
于![]() ,
,
由题意有![]() ∴
∴![]() ,则
,则![]()
而∠1=∠2,∴ ![]() =
=![]()
∴![]() ,即
,即![]() . …………………3分
. …………………3分
在Rt![]() 中,
中,![]() =
=![]() =
=![]() ,
,
而![]() ∽
∽![]() ,∴
,∴![]() , 即
, 即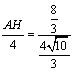 , ∴
, ∴![]() .
.
再连接![]() ,显然有
,显然有![]() ,
,
∴![]() .
.
所求![]() 的长为
的长为![]() . …………………3分
. …………………3分

练习册系列答案
相关题目