题目内容
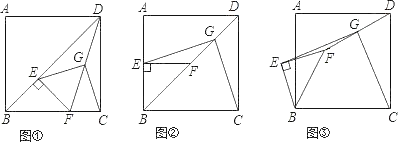
【题目】如图1,等边![]() 中,点
中,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,连
,连![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)如图2,延长![]() 至点
至点![]() ,使得
,使得![]() ,连
,连![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,连![]() ,
,![]() .若
.若![]() ,则
,则![]() ______.
______.
【答案】(1)详见解析;(2)![]()
【解析】
(1)先根据等边三角形的性质得出∠BAC=∠ACD=60°,AB=AC=BC,进而得出CD=AE,即可得出结论;
(2)先由△CAD≌△ABE,判断出∠CAD=∠ABE,进而得出∠AFE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,即可得出结论;
(3)先判断出∠BAF=∠CAG,进而判断出△ABF≌△ACG(SAS),得出∠AGC=∠AFB=180°-∠AFG=60°,判断出AD∥CG,即可得出结论.
解:(1)∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,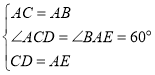 ,∴
,∴![]() ;
;
(2)由(1)知,![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() 是等边三角形;
是等边三角形;
(3)由(2)知,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,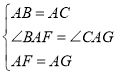 ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目