题目内容
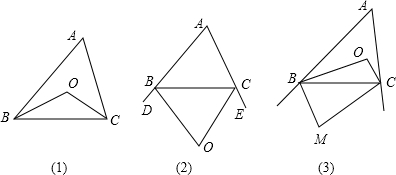
探索:(1)如图(1),在△ABC中,OB、OC分别是∠ABC、∠ACB的平分线.若∠A为x°,则∠BOC=
(2)如图(2),BO、CO为△ABC两外角∠DBC、∠BCE的平分线,若∠A为x°,则∠BOC=
(3)如图(3)O、M分别是△ABC的内外角平分线的交点,如果∠BOC:∠BMC=3:2,则∠A=
分析:(1)根据三角形角平分线的性质可得,∠BOC+∠OCB=90°-
,根据三角形内角和定理可得∠BOC=90°+
;
(2)根据三角形外角平分线的性质可得∠BCO=
(∠A+∠ABC),∠OBC=
(∠A+∠ACB),根据三角形内角和定理可得∠BOC=90°-
;
(3)根据(1)(2)的结论及三角形内角和定理可得x=36°.
| x° |
| 2 |
| x° |
| 2 |
(2)根据三角形外角平分线的性质可得∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
| x° |
| 2 |
(3)根据(1)(2)的结论及三角形内角和定理可得x=36°.
解答:解:(1)∵在△ABC中,OB、OC分别是∠ABC、∠ACB的平分线,∠A为x°,
∴∠BOC+∠OCB=
(180°-∠A)=
×(180°-x°)=90°-
,
故∠BOC=180°-(90°-
)=90°+
;
(2)∵BO、CO为△ABC两外角∠DBC、∠BCE的平分线∠A为x°,
∴∠BCO=
(∠A+∠ABC),∠OBC=
(∠A+∠ACB),
∴∠BOC=180°-∠BCO-∠OBC=180°-
[∠A+(A+∠ABC+∠ACB)]=180°-
(∠A+180°)=90°-
;
(3)设∠A=x°,
∵O、M分别是△ABC的内外角平分线的交点,由(1)(2)得∠BOC=90°+
.∠BMC=90°-
,
∵∠BOC:∠BMC=3:2,
即
=
,
即3(90°-
)=2(90°+
),
解得x=36°
则∠A=36°.
∴∠BOC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| x° |
| 2 |
故∠BOC=180°-(90°-
| x° |
| 2 |
| x° |
| 2 |
(2)∵BO、CO为△ABC两外角∠DBC、∠BCE的平分线∠A为x°,
∴∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠BCO-∠OBC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| x° |
| 2 |
(3)设∠A=x°,
∵O、M分别是△ABC的内外角平分线的交点,由(1)(2)得∠BOC=90°+
| x° |
| 2 |
| x° |
| 2 |
∵∠BOC:∠BMC=3:2,
即
90°+
| ||
90°-
|
| 3 |
| 2 |
即3(90°-
| x° |
| 2 |
| x° |
| 2 |
解得x=36°
则∠A=36°.
点评:此类题目比较简单,考查的是三角形内角与外角的关系,角平分线的性质,三角形内角和定理,属中学阶段的常规题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



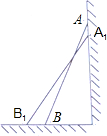 子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?