题目内容
 如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.
如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.
解: ∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,
∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,
∴存在线段AB且AB的位置已经固定,
当P和B重合时,x=4,即x≤4
当x=2,P和A重合,即x≥2,
∴x的取值范围是2≤x≤4,
如图,S矩形PNDM=xy,且2≤x≤4,
延长NP交EF于G,显然PG∥BF,
∴△AGP∽△AFB,
∴ ,
,
即 ,
,
∴y=- x+5,
x+5,
∴S=xy=- x2+5x,
x2+5x,
即S=- x2+5x(2≤x≤4).
x2+5x(2≤x≤4).
分析:矩形PMDN的面积=PM×PN,可构造相似三角形,利用相似三角形的性质得到y用x表示的关系式,代入前面所列式子即可.
点评:解决本题的关键是得到所求矩形的等量关系,难点是利用相似三角形的判定与性质得到y用x表示的关系式.
 ∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,
∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,∴存在线段AB且AB的位置已经固定,
当P和B重合时,x=4,即x≤4
当x=2,P和A重合,即x≥2,
∴x的取值范围是2≤x≤4,
如图,S矩形PNDM=xy,且2≤x≤4,
延长NP交EF于G,显然PG∥BF,
∴△AGP∽△AFB,
∴
 ,
,即
 ,
,∴y=-
 x+5,
x+5,∴S=xy=-
 x2+5x,
x2+5x,即S=-
 x2+5x(2≤x≤4).
x2+5x(2≤x≤4).分析:矩形PMDN的面积=PM×PN,可构造相似三角形,利用相似三角形的性质得到y用x表示的关系式,代入前面所列式子即可.
点评:解决本题的关键是得到所求矩形的等量关系,难点是利用相似三角形的判定与性质得到y用x表示的关系式.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
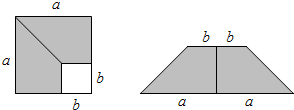

| A、(a-b)2=a2-2ab+b2 | B、(a+b)2=a2+2ab+b2 | C、a2-b2=(a+b)(a-b) | D、a2+ab=a(a+b) |

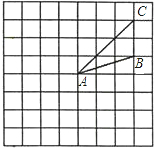 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离. 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.