题目内容
如图，在⊙O中，AB是⊙O直径，∠BAC=40°，则∠ADC的度数是
- A.40°
- B.50°
- C.60°
- D.80°
B
分析：AB是⊙O直径可得∠ACB=90°，再根据直角三角形的性质即可求解．
解答：∵AB是⊙O直径
∴∠ACB=90°
∵∠BAC=40°
∴∠D=∠B=90°-∠BAC=50°
故选B．
点评：本题考查圆周角定理和直角三角形的性质的运用．
分析：AB是⊙O直径可得∠ACB=90°，再根据直角三角形的性质即可求解．
解答：∵AB是⊙O直径
∴∠ACB=90°
∵∠BAC=40°
∴∠D=∠B=90°-∠BAC=50°
故选B．
点评：本题考查圆周角定理和直角三角形的性质的运用．
练习册系列答案
名校课堂系列答案
相关题目
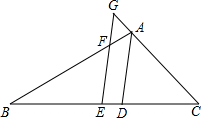如图，在△ABC中，AB＞AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．
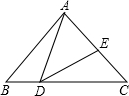如图，在△ABC中，AB=AC，D为BC边上一点，且∠BAD=30°，若AD=DE，∠EDC=33°，则∠DAE的度数为
如图，在△ABC中，AB=AC，D是△ABC内一点，且BD=DC．求证：∠ABD=∠ACD．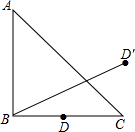
如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
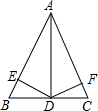如图，在△ABC中，AB=AC，D点是BC的中点，DE⊥AB于E点，DF⊥AC于F点，则图中全等三角形共有