题目内容
【题目】已知二次函数y=
+4x+6．
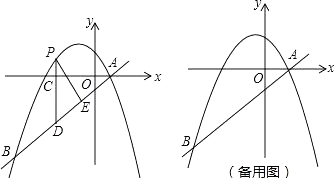
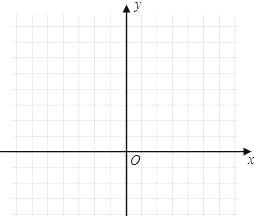
（1）求出该函数图象的顶点坐标，对称轴，图象与x轴、y轴的交点坐标，并在下面的网格中画出这个函数的大致图象；
（2）利用函数图象回答：
①当x在什么范围内时，y随x的增大而增大？当x在什么范围内时，y随x的增大而减小？
②当x在什么范围内时，y＞0？
【答案】(1) 顶点坐标（1，8）；对称轴为直线x=8；与x轴交点坐标（﹣1，0），（3，0）；与y轴交点坐标（0，6）；图象详见解析；(2)①当x≤1时，y随着x的增大而增大，当x≥1时，y随着x的增大而减小；
②当﹣1＜x＜3时，y＞0．
【解析】
试题分析：（1）顶点坐标为（
，
）对称轴是x=，与x轴的坐标y=0，与y轴的交点坐标x=0；
（2）①据对称轴的左侧还是右侧来进行判断函数值随自变量的变化；
②根据与x轴的交点来判断函数值大于0的情况．
试题解析：（1）∵a=﹣2，b=4，c=6，
∴=
=1，=
=8，
∴顶点坐标（1，8），对称轴为直线x=8，
当y=0时，
+4x+6=0，
∴
=3，
=﹣1，
当x=0时，y=6，
∴函数图象与x轴交点坐标（﹣1，0），（3，0），与y轴交点坐标（0，6）；
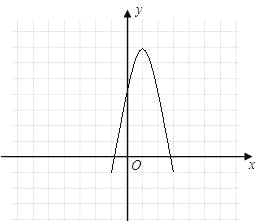
（2）由图象可知：
①当x≤1时，y随着x的增大而增大，当x≥1时，y随着x的增大而减小；
②当﹣1＜x＜3时，y＞0．
练习册系列答案
金状元绩优好卷系列答案
相关题目
