Question

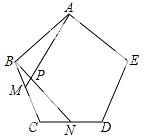
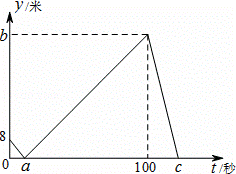
如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于G．

（1）若M为边AD中点，求证：△EFG是等腰三角形；

（2）若点G与点C重合，求线段MG的长；

（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．

Answer 1

长度，然后用含a的代数式表示△EFG的面积S，指出S的最小整数值．

又∵∠MCD+∠MFD=90°，∠AME+∠AEM=90°，∴∠AME=∠MCD.

∵∠MAE=∠CDM=90°，∴△MAE∽△CDM. ∴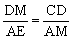，即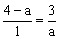，解得a=1或3.

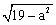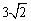代入CM=得CM=或.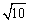

∵点G与点C重合，∴MG=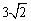或.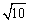

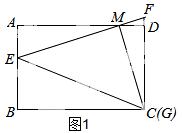
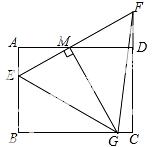
（3）①当点M在AD上时，如答图2，过点M作MN⊥BC交BC于点N，

∵AB=3，AD=4，AE=1，AM=a。∴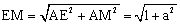，MD=AD-AM=4-a.

∵∠A=∠MDF=90°，∠AME=∠DMF，∴△MAE∽△MDF. ∴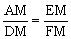，即.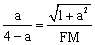

∴.∴.

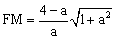∵AD∥BC，∴∠MGN=∠DMG.

∵∠AME+∠AEM=90°，∠AME+∠DMG=90°，∴∠AME=∠DMG. ∴∠MGN=∠AME.

②当点M在AD的延长线上时，如图3，过点M作MN⊥BC，交BC延长线于点N，

∵AB=3，AD=4，AE=1，AM=a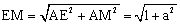，∴，MD=a-4.

∵DC∥AB，∴△MAE∽△MDF.∴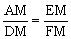，即.∴.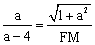

∴.

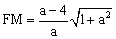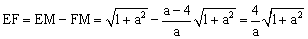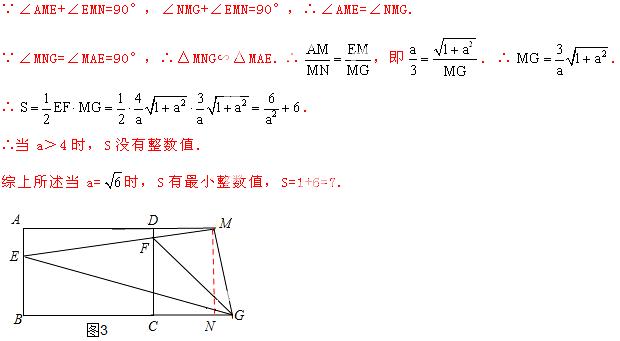
考点：1.单动点问题；2.矩形的性质；3.全等三角形的判定和性质；4. 等腰三角形的判定和；5.勾股定理；6.相似三角形的判定和性质；7.分类思想的应用.