题目内容
 已知:如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF,CF,∠D=∠BFC.
已知:如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF,CF,∠D=∠BFC.(1)求证:AD是⊙O的切线;
(2)当CF∥AB时,求∠D的度数.
考点:切线的判定
专题:
分析:(1)由OD⊥AC,∠D=∠BFC与圆周角定理,易求得∠EAD+∠BAC=90°,即可证得AD是⊙O的切线;
(2)由CF∥AB,易证得
=
=
,继而求得答案.
(2)由CF∥AB,易证得
 |
| AF |
 |
| CF |
 |
| BC |
解答:(1)证明:∵OD⊥AC,
∴∠AED=90°,
∴∠EAD+∠D=90°,
∵∠D=∠BFC,∠BFC=∠BAC,
∴∠BAC=∠D,
∴∠EAD+∠BAC=90°,
即OA⊥AD,
∴AD是⊙O的切线;
(2)∵CF∥AB,
∴∠BFC=∠B,
∴
=
,
∵OD⊥AC,
∴
=
,
∴
=
=
,
∴∠AOF=
×180°=60°,
∴∠D=∠ABF=
∠AOF=30°.
∴∠AED=90°,
∴∠EAD+∠D=90°,
∵∠D=∠BFC,∠BFC=∠BAC,
∴∠BAC=∠D,
∴∠EAD+∠BAC=90°,
即OA⊥AD,
∴AD是⊙O的切线;
(2)∵CF∥AB,
∴∠BFC=∠B,
∴
 |
| BC |
 |
| AF |
∵OD⊥AC,
∴
 |
| AF |
 |
| CF |
∴
 |
| AF |
 |
| CF |
 |
| BC |
∴∠AOF=
| 1 |
| 3 |
∴∠D=∠ABF=
| 1 |
| 2 |
点评:此题考查了切线的判定以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( )
如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在直角△ABC中,∠C=90°,DE⊥AB于E,AD平分∠BAC交BC于点D,若CD=4,则ED=
如图,在直角△ABC中,∠C=90°,DE⊥AB于E,AD平分∠BAC交BC于点D,若CD=4,则ED=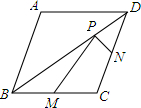 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.
已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点.