题目内容
如图所示，梯形ABCD中，AD∥BC，AB=DC．（1）P，E，F分别是BC，AC，BD的中点，求证：AB=PE+PF；
（2）如果P是BC上的任意一点（中点除外），PE∥AB，PF∥DC，那么AB=PE+PF，这个结论还成立吗？如果成立，请证明；若不成立，请说明理由．
分析：（1）由P，E，F分别是BC，AC，BD的中点，很容易想到中点连成中位线，利用三角形中位线定理和AB=CD，结论可证．
（2）P是BC上的任意一点（中点除外），PE∥AB，PF∥DC，有此关系，说明AB=PE+PF是否成立，首先想到平行线分线段成比例定理，列出线段的比例关系，
=
①，
=
②，利用合理的等式变形，①②的左边+左边=右边+右边，可得
=1，从而问题得到解决．
（2）P是BC上的任意一点（中点除外），PE∥AB，PF∥DC，有此关系，说明AB=PE+PF是否成立，首先想到平行线分线段成比例定理，列出线段的比例关系，
| PE |
| AB |
| PC |
| BC |
| PF |
| CD |
| PC |
| BC |
| PE+PF |
| AB |
解答：（1）证明：∵P，E，F分别为中点，
∴PE=
AB，PF=
CD．（三角形中位线定理）
∴PE+PF=
（AB+CD）．
又∵AB=CD，
∴AB=PE+PF．
（2）成立．
∵PE∥AB，PF∥CD，
∴
=
，
=
，（平行线分线段成比例定理）
∵AB=CD
∴
+
=
+
∴
=
=
=1，
∴
=1，
∴PE+PF=AB．
∴PE=
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PF=
| 1 |
| 2 |
又∵AB=CD，
∴AB=PE+PF．
（2）成立．
∵PE∥AB，PF∥CD，
∴
| PE |
| AB |
| PC |
| BC |
| PF |
| CD |
| PB |
| BC |
∵AB=CD
∴
| PE |
| AB |
| PF |
| CD |
| PC |
| BC |
| PB |
| BC |
∴
| PE+PF |
| AB |
| PC+PB |
| BC |
| BC |
| BC |
∴
| PE+PF |
| AB |
∴PE+PF=AB．
点评：此题主要考查三角形中位线定理和平行线分线段成比例定理的理解及运用．等式的合理变形也是问题解决的好方法．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图所示，在△ABC中，AB=AC，BD，CE分别为∠ABC，∠ACB的平分线．
已知：如图所示，梯形ABCD中，AD∥BC，BD平分∠ABC，∠A=120°，BD=BC=4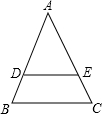
如图所示，在△ABC中，DE∥BC，△ADE和梯形DBCE的面积相等，则AD：DB=
梯形的边运动，设点P运动的路程为x，△ABP的面积为y，函数图象如图②所示，则△ABC面积为